どうも!予備校で物理を楽しく教えている『フィズ丸』です!(^^)!
高校物理の電磁気分野の初めに『ガウスの法則』という法則がありますね!
この法則は問題で見る機会はあるのですが、参考書でわかりやすくまとめていて、使い方までまとめているものがほとんどないです。
ちゃんと教わっていないのでガウスの法則がわからないという相談を毎年多く受けます。
物理が得意な生徒でもちゃんと理解して使いこなせている生徒ってなかなかいないですよね。
なので、大学入試の問題でガウスの法則をもとにした問題が出題されると、その問題が解けるだけで一気に合格ラインを超えられたりします!(^^)!
今回の記事では、他の参考書には載っていない、私が予備校で教えているマル秘の方法をガウスの法則を理解して使えるようにまとめてみました!
特にガウスの法則を理解して使えるようにするために必要なことは
- 電気力線の性質を理解する
- ガウスの法則はどういうときに使うのかを理解する
- ガウスの法則の使い方を理解する
- ガウスの法則の練習問題で練習する
この4点をしっかりと抑えていきましょう!
そうすれば必ずガウスの法則が理解できて、問題も解けるようになります!
そして、ガウスの法則は使えるようになると、電場の分野の理解が一気に深くなり、入試問題も後半までしっかりと解けるようになるのでしっかりと読んで理解してくださいね!
Contents
電場の定義

まずはじめは『電場』の定義です。
電場の定義は2つあるので、この分野がわからない生徒はしっかりと言葉の定義を理解しましょう!
《電場の定義》
- 電荷が力を受ける空間(場)
- +1〔C〕の点電荷が受ける静電気力
電場の定義①:電荷が力を受ける空間(場)
まず1つ目の定義『電荷が力を受ける空間』ですが、今、私たちが住んでいる空間は『質量が力を受ける空間』ですよね?
質量$m$の物体には地球表面上であれば$mg$の重力を、地球の中心から$r$だけ離れていれば$G\frac{mM}{r^{2}}$の万有引力を受ける空間になりますよね。
それと同じで、電場とは『電荷が力を受ける空間』なんです。
- 重力がはたらく空間を『重力場』っていうよ!
- 電場の強さ$E$は、重力場では重力加速度$g$のようなイメージを持っておこう!
力学では『重力(万有引力)ってなんではたらくの?』って、疑問に思わずに物理を学んでいる人が大勢いますよね。
それと同じで電荷が力を受ける空間があるので、高校物理の範囲内ではあまり疑問を持たずに勉強していこう!
電場の定義②:+1〔C〕の点電荷が受ける静電気力
2つ目の定義が『+1〔C〕の点電荷が受ける静電気力』です!
なので電場の単位は〔N/C〕になりますね!
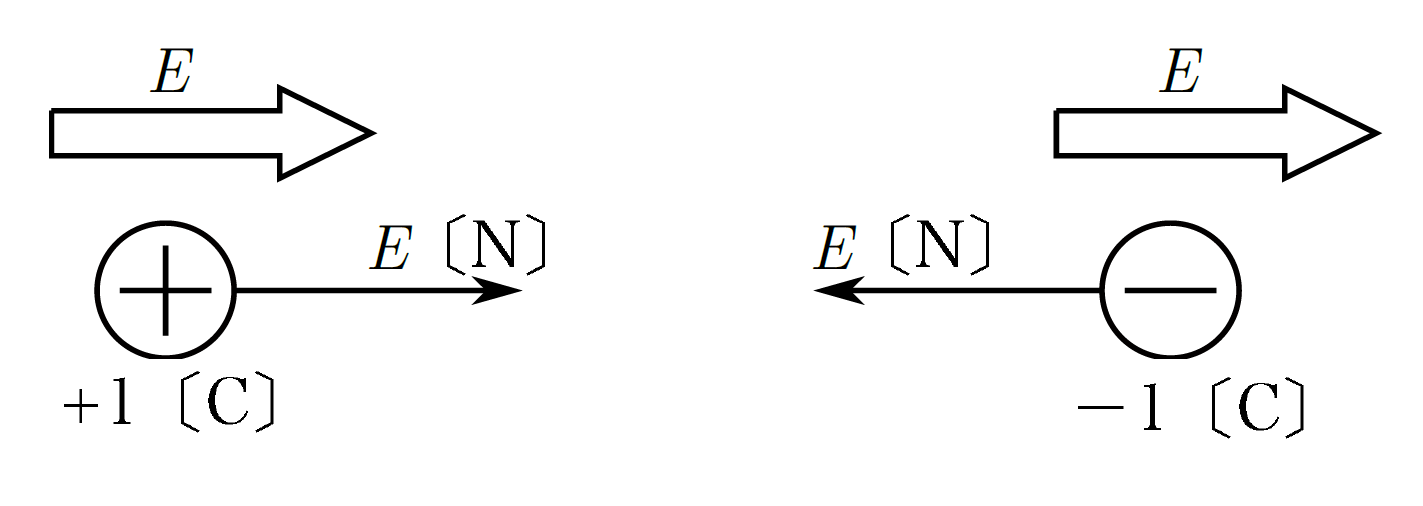
つまり、電場$E$〔N/C〕の場所に$+1$〔C〕の点電荷を置くと、その点電荷は電場の向きに$E$〔N〕の大きさの力を受けるということです!
少し考えにくいですが、電場$E$〔N/C〕の場所に$-1$〔C〕の点電荷を置くと、受ける力の大きさは$E$〔N〕ですが、向きが逆になります。
これはしっかりと覚えておきましょう!
重力に置き換えてみると、地球表面上に+1〔kg〕の物体を置くと$g$〔N〕の力を受けることと一緒だね!
電気力線って何??

電気力線は学校でも習いますが、あまり意識せずに問題を解く生徒が多いですよね。
でも電気力線をしっかりと理解しておくと、縁の下の力持ちのような役割をしてくれて、
- ミスに気付くことができる
- 問題を解く指針になる
ことがあるんです!
ガウスの法則を理解するうえで電気力線の性質の理解は必須なので、しっかりと理解しよう!
まず
- 電気力線の性質
- 点電荷が作る電気力線の概形
- 帯電した平行極板が作る電気力線の概形
の3点を確認していきましょう!
電気力線の性質
まずは電気力線の性質に着目してみましょう!
この性質の順は私の経験から大学入試にとって重要度の高い順に並べています。
《電気力線の性質》
- 電気力線は高電位から低電位の向きになる。
- 電気力線の密度が電場の強さを表す。
- 電気力線の接戦方向が電場の向きになる。
- 電気力線は正の電荷から出て負の電荷に入る。
- 電気力線どうしは反発する。
- 電気力線は交わったり折れ曲がったりしない。
- 電気力線は電荷がないのに発生しない。また急に消滅することもない。
この7つの性質があります。
ただ、入試で重要なのが①から④なので、この4つはしっかりと覚えておきましょう!
特にガウスの法則を理解するうえで重要なのは②になりますね!
ではこの性質を意識して電気力線の図の具体例を見てみましょう!
点電荷が作る電気力線の概形を確認しよう!
まずは点電荷が作る電気力線を見ていきましょう!
矢印を付した実線で電気力線を書いてみると、下図のようになります。
正に帯電した点電荷と負に帯電した点電荷が作る電気力線はそれぞれ図a、bで、電気量の大きさの等しい、符号の異なる2つの点電荷が作る電気力線が図cになります。
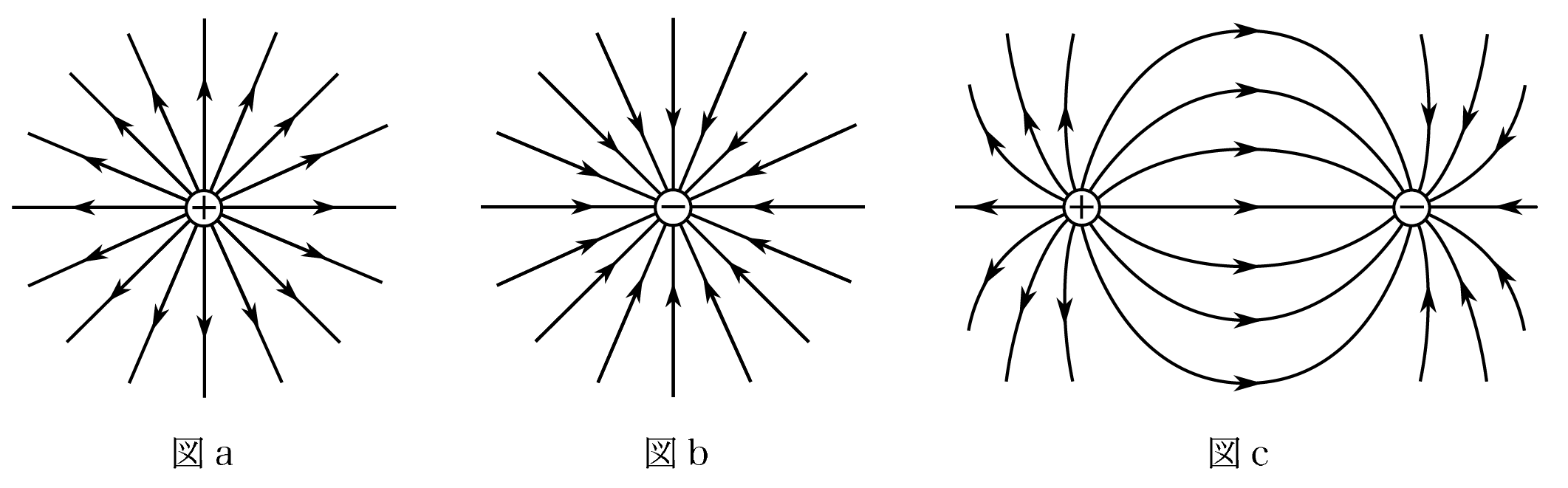
この図で着目する点は
- 電気力線は高電位から低電位の向きに矢印が向く
- 電気力線が密なところほど電場が強い
- 電気力線の接線方向が電場の向き
- 電気力線は正電荷から出て、負電荷に入る
この4点はしっかりと読み取れるようにしておきましょう!
下に4つの着目点説明をそれぞれ入れておきますね!
- 特に図cでは正電荷の場所が高電位、負電荷の場所が高電位となっています。
- 点電荷に近いところほど電気力線が密になっているので電場が強く、点電荷から離れるほど電気力線の間隔が狭くなっているので電場は弱くなっています。
- 図a,bは直線なので電気力線の向きが電場の向き、図cは曲線なので、各点の接線方向が電場の向きになっています。
- そのまんまです(笑)。
帯電した平行極板が作る電気力線の概形を確認しよう!
次に帯電した平行極板が作る電気力線です。
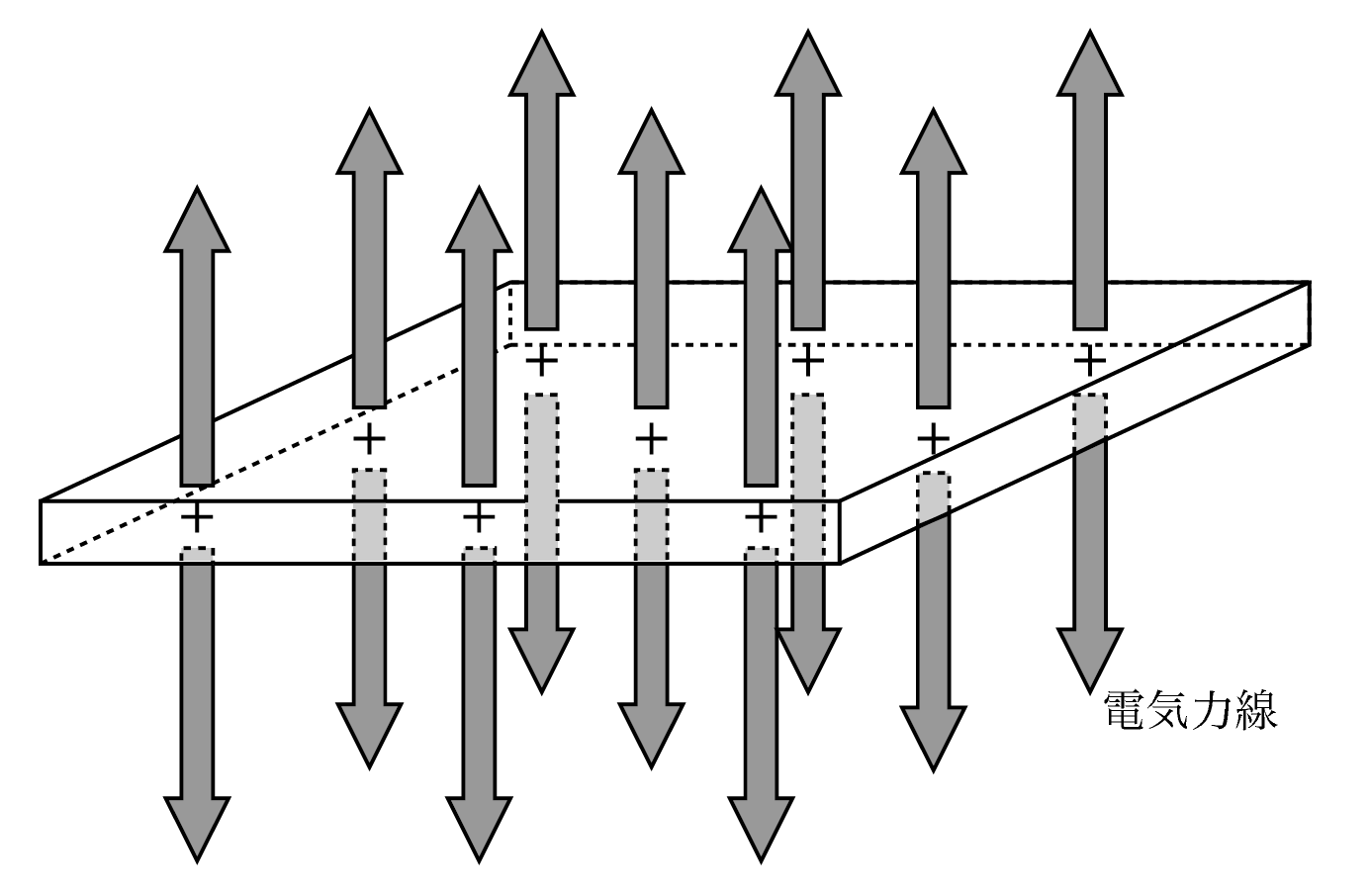
例えば、正に帯電した平行極板だと、上図の矢印ように(近似的に)平行な電気力線ができます。
この図で着目する点は
- 電気力線の密度は等しいので、どの場所でも電場の強さが等しい
- 電気力線の接線方向が電場の向きなので、極板に垂直方向が電場の向きになる
この2点はしっかりと読み取れるようにしておきましょう!
ガウスの法則って何??

ようやくこの記事のメインテーマである『ガウスの法則』ですね。
ではまず最初にガウスの法則って結局何の法則なんでしょうか?
答えは簡単です。
《ガウスの法則》
電場の強さを求める法則
です。
電気量$Q$の点電荷が点電荷から距離$r$の位置に作る電場の強さの公式は$E=k\Large{\frac{|Q|}{r^{2}}}$、コンデンサーの極板間の電場はの公式は$E=\Large{\frac{Q}{\varepsilon S}}$でしたよね?
これはただただ覚える式ではなく、実はすべての電場の式はガウスの法則から求められるんです。
なので、正直なところガウスの法則が使えれば公式を覚える必要はなくなるわけですが・・・。
ただ入試となるとやはり効率よく解かないと合格は厳しくなります。
『点電荷が作る電場』と『コンデンサーの極板間の電場』の公式はしっかりと覚えておきましょう!
ガウスの法則の約束

ガウスの法則を使う上で、高校物理の場合は約束を2つほどします。
なんで約束?って思うかもしれませんが、詳しくは大学の電磁気学で勉強する内容なので、ひとまず高校物理ではガウスの法則が使えるようになろうっていう意図です。
なので今から説明する2つの約束はとりあえず覚えればいいです。
《ガウスの法則の約束①》
$Q$〔C〕の電気量から出る電気力線の本数$N$は$$N=4\pi kQ=\frac{Q}{\varepsilon}$$
※$\varepsilon$は誘電率という物理量で、誘電分極のしやすさを表します。
《ガウスの法則の約束②》
面積$S$を垂直に貫く電気力線の本数を$N$とすると、電場の強さ$E$は$$E=\frac{N}{S}$$つまり、$$\mathrm{(電場の強さ)=(電気力線の密度)}$$
この約束②は電気力線の性質②を表すので、ガウスの法則の約束は①だけ教える人も多いです。
しかし、結局②を使って電場の強さを求めるので、再度確認のためここで約束として覚えてもらうようにしています。
なので、この2つの約束はしっかりと覚えておきましょう!
ガウスの法則はこの4Stepで使えるようになる!

大体の参考書や問題集はガウスの法則を①だけ説明してそのまま問題を解いていく感じですが、正直言ってそれだけではガウスの法則を使えるようにならないです。
なので、ここではガウスの法則を使えるようにするために、使い方を4Stepでかいていきます!
この4Stepを順に進めていくと、ガウスの法則をすぐ使えるようになるので、しっかりとマスターしよう!
ガウスの法則を求める4Step
Step1:電気力線に垂直になるように閉曲面をとる!
Step2:閉曲面の表面積$S$を求める!
Step3:約束①を用いてを貫く電気力線の総本数$N$を求める!
Step4:ガウスの法則の約束②に代入する!
Step2~4は難しくないのですが、Step1が難所なので、その説明をしていきますね!
《Step1の説明》
高校物理で出てくる電気力線の概形は次の4つだけなので、まずはその概形を覚えましょう!
- 点電荷(図1)
- 帯電した平板導体(図2)
- 帯電した導体棒(図3)
- 帯電した導体球(図4)
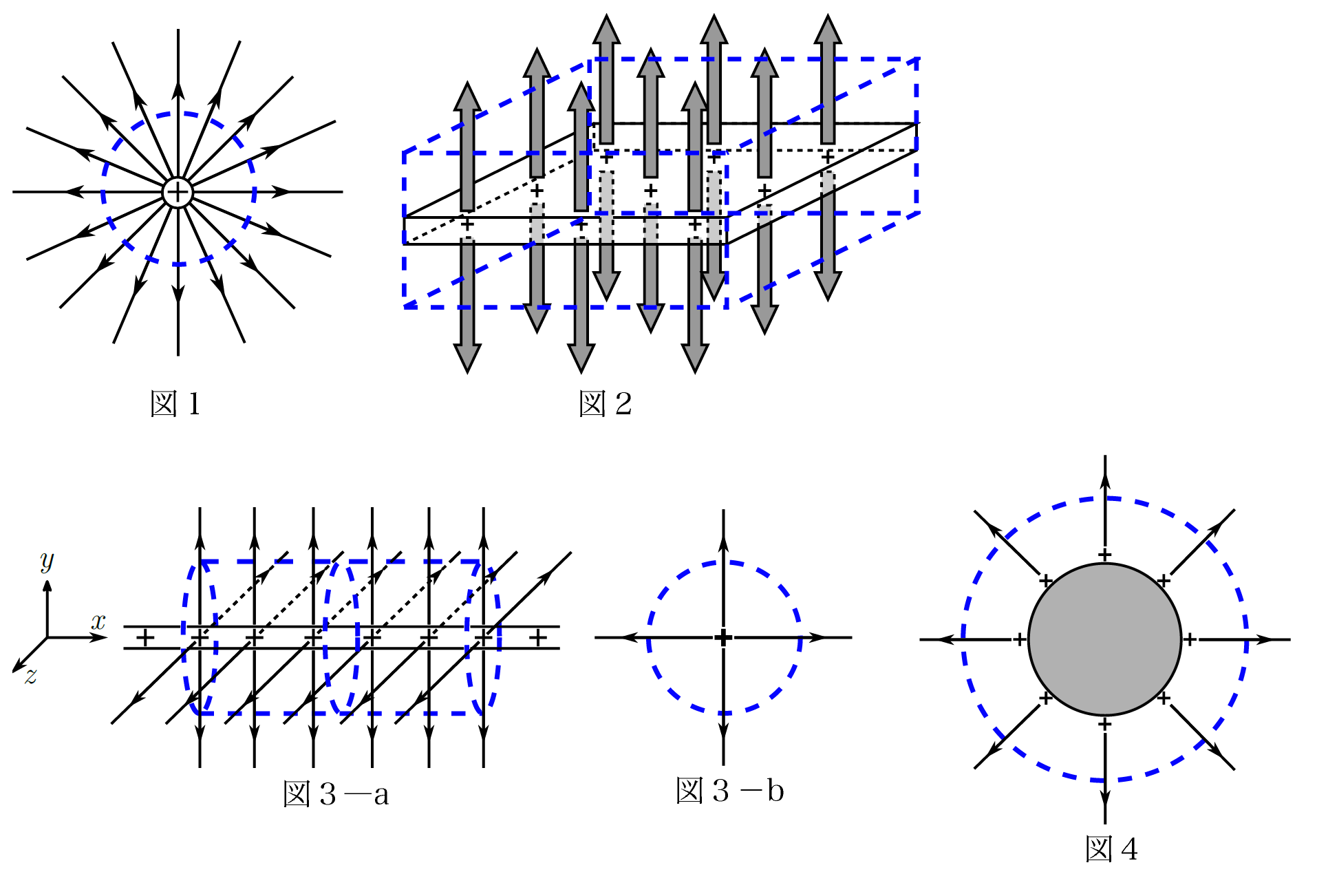
上図の図1~4の矢印が電気力線、青い点線が閉曲面となります。
電気力線の概形は理解はできますが、覚えた方がいいです。
そしてその電気力線に垂直になるように閉曲面を取ります。
ちなみに図3の帯電した導体棒に関しては、$x$軸正方向から見た図を図3-bに示しておきます。
具体例でガウスの法則を使えるようになろう!

では上でまとめた4Stepを使って具体例を4つ解いていきましょう!
この4つの例は入試でも見かけるのでしっかりと解けるようにしていこう!
例題1:点電荷が作る電場を求めてみよう!
《問題》
正の電気量$Q$に帯電した点電荷から距離$r$離れた点の電場の強さ$E$を求めよ。
この問題を4Stepに沿って解いていきましょう!
《解答》
Step1:電気力線に垂直になるように閉曲面をとる!
⇒下図の青い点線のように、電気力線に垂直になるように閉曲面をとると、球形の閉曲面をとります。
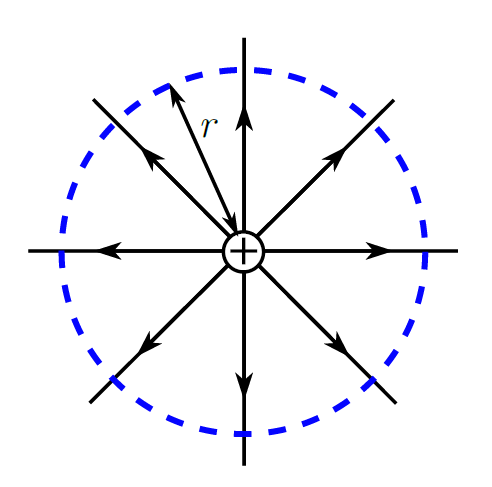
Step2:閉曲面の表面積$S$を求める!
⇒Step1の閉曲面は半径$r$の球なので、表面積$S$は$S=4\pi r^{2}$となります。
Step3:約束①を用いて閉曲面を貫く電気力線の総本数$N$を求める!
⇒約束①より、$N=4\pi kQ$本となります。
Step4:Step2とStep3をガウスの法則の約束②に代入する!
⇒約束②より、$$E=\frac{N}{S}=\frac{4\pi kQ }{4\pi r^{2}}$$ $$\therefore E=k\frac{Q}{r^{2}}$$となります。
例題2:帯電した球形導体が作る電場を求めてみよう!
《問題》
正の電気量$Q$に帯電した半径$R$の導体球の中心から距離$r$(>$R)$離れた点の電場の強さ$E$を求めよ。
この問題を4Stepに沿って解いていきましょう!
《解答》
Step1:電気力線に垂直になるように閉曲面をとる!
⇒下図の青い点線のように、電気力線に垂直になるように閉曲面をとると、球形の閉曲面をとります。
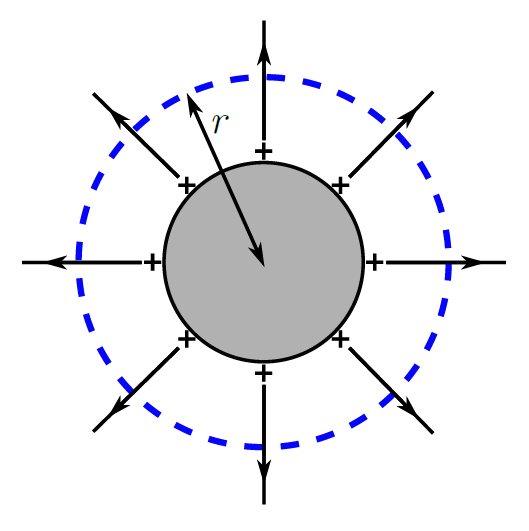
Step2:閉曲面の表面積$S$を求める!
⇒Step1の閉曲面は半径$r$の球なので、表面積$S$は$S=4\pi r^{2}$となります。
Step3:約束①を用いて閉曲面を貫く電気力線の総本数$N$を求める!
⇒約束①より、$N=4\pi kQ$本となります。
Step4:Step2とStep3をガウスの法則の約束②に代入する!
⇒約束②より、$$E=\frac{N}{S}=\frac{4\pi kQ }{4\pi r^{2}}$$ $$\therefore E=k\frac{Q}{r^{2}}$$となります。
導体球が作る電場の強さは点電荷の式と同じになるよ。そこは覚えておこう!
例題3:帯電した平板導体が作る電場を求めてみよう!
《問題》
十分広く、薄い平面導体板の面積$S$の部分に正の電気量$Q$が一様に分布している。この平面導体板の表面から距離$r$だけ離れた位置の電場の強さ$E$を求めよ。
この問題を4Stepに沿って解いていきましょう!
《解答》
Step1:電気力線に垂直になるように閉曲面をとる!
⇒下図の青い点線のように、電気力線に垂直になるように閉曲面をとると、直方体形の閉曲面をとります。
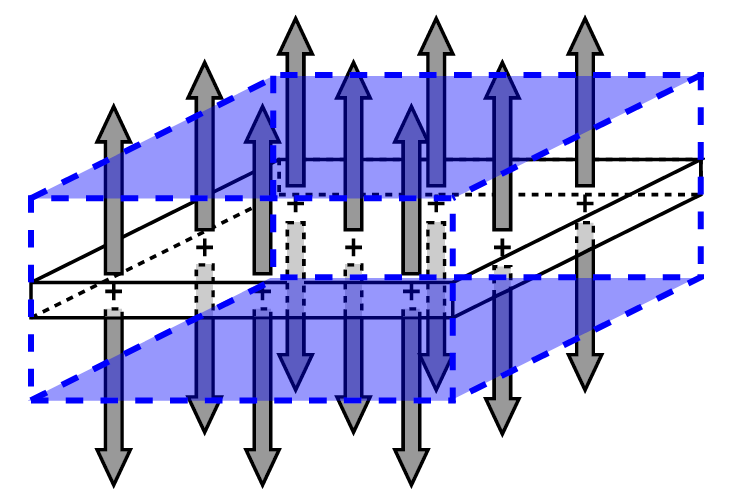
Step2:閉曲面の表面積$S$を求める!
⇒Step1の閉曲面は直方体で、直方体の青く塗られている面の面積を$S$とすると、電気力線が貫いている面積は上下の$2S$となることがわかります。この面積は$r$によらないのもわかりますね。
Step3:約束①を用いて閉曲面を貫く電気力線の総本数$N$を求める!
⇒約束①より、$N=4\pi kQ=\frac{Q}{\varepsilon}$本となります。
Step4:Step2とStep3をガウスの法則の約束②に代入する!
⇒約束②より、$$E=\frac{N}{S}=\frac{\frac{Q}{\varepsilon}}{2S}$$ $$\therefore E=\frac{Q}{2\varepsilon S}$$となります。
この内容はコンデンサーの極板間の電場を求めるときに用いるので、しっかりと理解しておこう!
例題4:帯電した導体棒が作る電場を求めてみよう!
《問題》
十分長く細い導体棒に単位長さ当たり$\rho$の正の電荷が一様に分布している。この導体棒から距離$r$だけ離れた点での電場の強さ$E$を求めよ。
この問題を4Stepに沿って解いていきましょう!
《解答》
Step1:電気力線に垂直になるように閉曲面をとる!
⇒下図の青い点線のように、電気力線に垂直になるように閉曲面をとると、円柱形の閉曲面をとります。
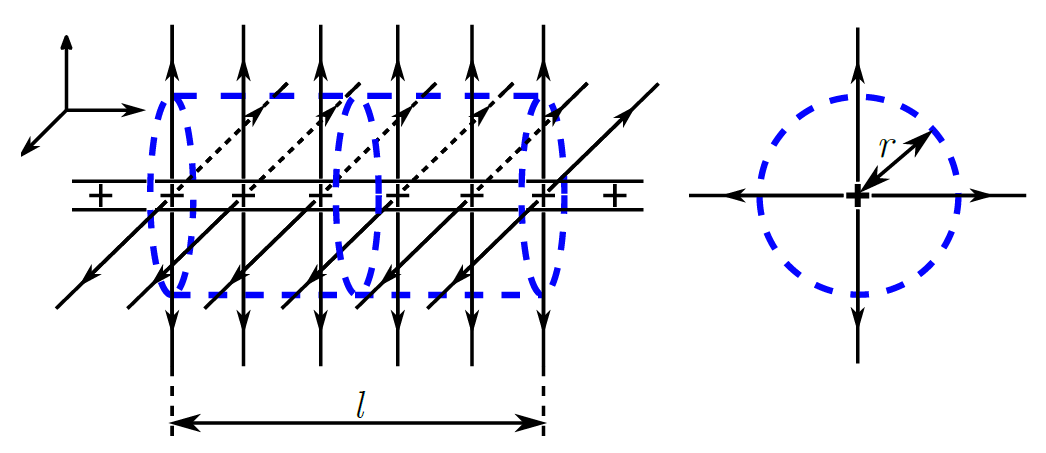
Step2:閉曲面の表面積$S$を求める!
⇒Step1の閉曲面は半径$r$の円を持つ円柱で、高さを$l$とすると、電気力線が貫いている面の表面積$S$は$S=2\pi r\times l$となります。
Step3:約束①を用いて閉曲面を貫く電気力線の総本数$N$を求める!
⇒長さ$l$の導線に分布している電気量は$\rho l$となるので、約束①より、$N=4\pi k\rho l$本となります。
Step4:Step2とStep3をガウスの法則の約束②に代入する!
⇒約束②より、$$E=\frac{N}{S}=\frac{4\pi k\rho l }{2\pi lr }$$ $$\therefore E=\frac{2k\rho}{r}$$となります。
まとめ

これで『ガウスの法則をわかりやすく使い方まで解説!永久保存版!』の記事を終わりにします。
ガウスの法則はなかなかわかりやすく説明してくれいてい参考書や問題集はないのです。
これだけガウスの法則についてまとめている記事も本当にないです。
なので、是非この記事を何度も読んで、何度も例題1~4を解いてガウスの法則を何度も解いて、ガウスの法則を得意にして下さい!
そうすれば周りの受験生よりも1歩も2歩も先に進めます!
また、このサイトではほかにも
・位置エネルギーの証明

・難関大学の対策方法
なども人気があるので是非読んでみて下さい!