こんにちは!
大手予備校で物理を教えているフィズ丸です!(^^)!
学校で『仕事とエネルギーの分野』を学んで、すごく多い意見として、
仕事が何なのかわからない。
仕事の求め方がわからない。
仕事とエネルギーの違いがわからない。
仕事とエネルギーのイメージができない。
仕事とエネルギーの関係がわからない。
このような質問や相談は毎年かなり多いです。
まぁ確かにこの分野は予備校講師の人でも教えるのになかなかてこずる人は多いですね!
なので、今回はテーマは
仕事とエネルギーを徹底理解する
です!
ただ、このテーマだけではざっくりしているので(笑)、もっとテーマを細分化して見てみると、
- 仕事の意味がわかるようになる。
- 仕事の求め方がわかるようになる。
- 仕事とエネルギーの違いがわかるようになる。
- 仕事とエネルギーのイメージができるようになる。
- 仕事とエネルギーの関係がわかるようになる。
この記事でこのような5点がわかるようになります!
仕事とエネルギーの分野は力学、熱力学、電磁気学、原子の4分野でずーっと重要になります!
高校物理の分野は力学、波動、熱力学、電磁気学、原子の5分野あるので、そのうちの4分野です!
(仕事とエネルギーの分野がわからない)=(物理がわからない)
と言っても過言ではないくらい重要な分野です!
なので、この分野をしっかりと理解して物理をできるようにしていきましょう!!
また、この記事でしっかりと理解した人は、後は選び抜かれた問題集でガンガン演習をする必要があります。
その問題演習として、進研ゼミの高校講座はすごくお勧めです!
進研ゼミは問題をかなり精選し、必要最低限の問題数で実力をつけられるので、資料請求からでもいいのでやってみてください!
Contents
仕事の定義をまずはしっかりと抑えよう!

仕事の意味が分からない人は、まず仕事の定義をしっかりと理解しましょう!
仕事の定義は2つあり、どっちもかなり重要な定義となるので、しっかりと抑えておきましょう!
定義①:仕事は力の距離的影響力を表す物理量
仕事の定義①:仕事は力の距離的影響力を表す物理量
ちょっと難しい表現ですが、つまりは
『その力がどれだけその物体を移動させたか』
というのが仕事の定義①です!
なので移動に関係ない力(移動方向と垂直関係にある力)がする仕事は0ということになりますね!
定義②:仕事はエネルギーを変化させる物理量
仕事の定義②:仕事はエネルギーを変化させる物理量
つまり、仕事をした分だけエネルギーが変化するということです(ほとんどそのまま(笑))。
この定義②を理解して頭に入れておかないと、物理全体として理解できない部分がかなり多くなる重要な定義です!
詳しくは後の『仕事とエネルギーの関係』でやりますが、ひとまず簡単な具体例でみておきましょう!
(具体例1)
1000Jのエネルギーをもっていた物体に200Jの仕事をすると、その物体は1200Jのエネルギーをもっているということです!
(具体例2)
1000Jのエネルギーをもっていた物体に-200Jの仕事をすると、その物体は800Jのエネルギーをもっているということです!
この2つの具体例のように仕事をすることによって、その物体が持っているエネルギーが変化します!
仕事の符号の求め方を理解しよう!

2つ目は『仕事の符号の求め方を理解しよう!』です。
これはとても簡単なので、仕事の符号は瞬時に判断できるように練習しましょう!
《仕事の符号の判断方法!》
物体の進んでいる方向に対して、
- 同じ向きの力は正の仕事をする。
- 逆向きの力は負の仕事をする。
です!
では、具体例で実際に符号を見てみましょう!
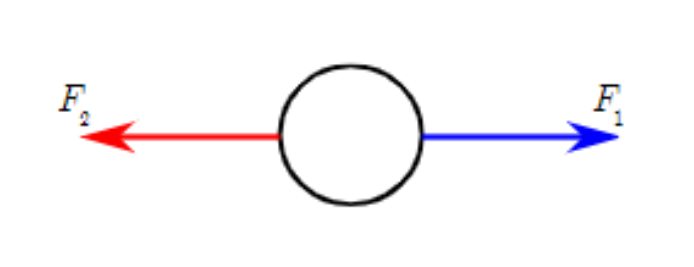
図のように、図の右向きに進んでいる物体があり、その物体に水平面から$\theta$の向きに大きさ$F_{1}$の力が、左向きに大きさ$F_{2}$の力がはたらいているとします。このとき、各力のする仕事の符号を求めてみましょう!
$F_{1}$は水平成分$F_{1}\cos\theta$は物体の進む方向の力となるので、$F_{1}$は正の仕事をします。
次に、$F_{2}$は物体が進む方向と逆向きの力となるので、$F_{2}$は負の仕事をします。
仕事の符号の判断方法はこれだけです!
仕事の求め方はこの3種類!

では続いて仕事の求め方です!
仕事を求める問題は苦手な人が大勢いるので、今から説明する3つの求め方を理解して覚えて対応できるようにしましょう!(^^)!
求め方①:$W=Fx$を用いる。
$W=Fx$はいつでも使えるかというとそうではないんです!
$W=Fx$使える条件
$F$が一定のときのみ$W=Fx$は使える。
この条件をしっかりと理解して、$F$が一定で、移動距離がわかっているときはこの求め方で求めましょう!
練習問題
ではその使い方を実際に見てみましょう!
物理は原理や公式を教えてもらったら、必ずその公式の使い方を確認しておかないと問題が解けませんからね!
(問題)
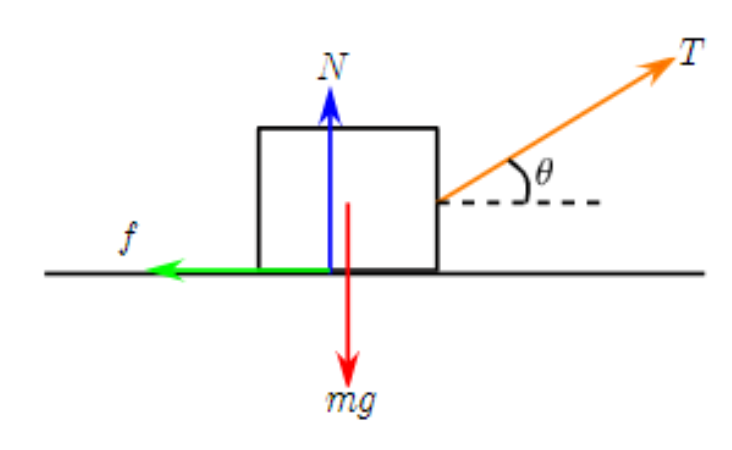
図のように、あらい水平面に置かれた質量$m$の物体に糸をつけ、糸が水平方向から$\theta$だけ傾く角度で一定の力で引っ張り、物体を距離$l$だけ移動させる。このとき、重力$mg$、垂直抗力$N$、動摩擦力$f$、張力$T$がする仕事をそれぞれ求めよ。
(解答)
まず、重力$mg$と垂直抗力$N$は進行方向に対して垂直なので、仕事は0になります。
次に、動摩擦力は進行方向と逆向きになっているため、負の仕事をします。
また、動摩擦力は一定の力なので、$W=Fx$より、動摩擦力のする仕事$W_{\mu}$は$$W_{\mu}=-fl$$となります。
最後に張力の仕事ですが、張力の進行方向成分は$Tcos\theta$となり、この力は進行方向の力かつ、一定の力なので、$W=Fx$より、張力の仕事$W_{\mathrm{ T }}$は$$W_{\mathrm{ T }}=Tcos\theta \times l$$となります。
求め方②:仕事の大きさ$W=$($F-x$グラフの面積)
2つ目ですが、
仕事の大きさ$W=$($F-x$グラフの面積)
この求め方は$F$が一定でも一定でなくても力$F$と位置$x$のグラフさえわかっていれば仕事を求めることができます。
ではなぜ$F-x$グラフの面積が仕事の大きさ$W$を表すのでしょうか。
例を用いて考えてみましょう!
$F-x$グラフの面積が仕事の大きさを表す理由
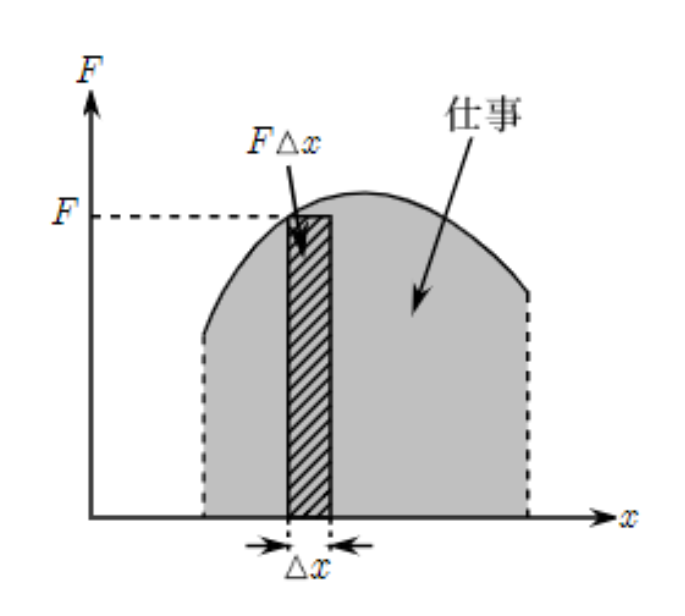
図の$F-x$グラフのように、力$F$が変化したとします。
このとき、途中の微小区間$\Delta x$だけ物体が移動したとします。
ここで、微小区間$\Delta x$だけ移動するときは、力は変化しないと近似できます。(ちょっと難しいですが、入試ではたびたび出てきます。)
なので、このときこの力がした仕事$\Delta w$は、$F$が一定なので、$$w=F\Delta x$$となります。
これは図の短冊部分の面積になりますよね!
この微小の面積を足していくと、それは近似的に$F-x$グラフの面積を表すので、
『$F-x$グラフの面積が仕事の大きさ$W$を表す』
ことがわかりますね!
求め方③:$W=$(エネルギーの変化量)
これは『仕事の定義②:仕事はエネルギーを変化させる物理量』でお伝えした通りです!(^^)!
仕事をすると、その分エネルギーが変化するんでしたね!
仕事を求める手順を抑えよう!

実際に仕事を求めてみるときは、次の2Stepで求めるようにしましょう!
Step1:仕事の符号を判断しよう!
Step2:仕事の大きさを求めよう!
この手順を使って、実際に具体例を用いて練習してみましょう!
具体例で練習してみよう。
(問題)
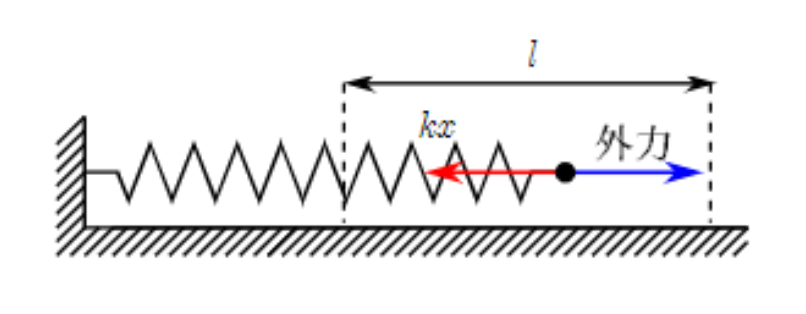
ばね定数$k$のばねに外力を加え、自然長から$l$だけ伸ばすとき、弾性力のした仕事$W_{k}$を求めよ。
(解答)
Step1:仕事の符号を判断しよう!
ばねは伸びるている最中なので、ばねの運動方向は伸びる方向と考えることができます。
この伸びる方向に対して弾性力は逆向きの力なので、弾性力の仕事は負の仕事となります。
まずはこれを判断できるようにしましょう!
Step2:仕事の大きさを求めよう!
弾性力は位置$x$によって変化する力なので、一定でない力となります。
よって、一定でない力がする仕事は$F-x$グラフの面積で求めます。
弾性力は$F=kx$と表されるので、$F-x$グラフの面積は直角三角形の面積なので$$\frac{1}{2}kx^{2}$$となることがわかりますね!
以上の2つのStepから、弾性力のした仕事$W_{k}$は$$W_{k}=-\frac{1}{2}kx^{2}$$となりますね!
このように、仕事はStep1で仕事の符号考え、Step2で仕事の大きさを考えることで求めることができます。
皆さんも是非この2Stepを意識しながら解いてみてください!
この方法は私が考え付いたことで、この例ができれば基本的にすべての力の仕事が求められるので、是非やってみてください!(^^)!
仕事とエネルギーの関係を理解しよう!

最後が『仕事とエネルギーの関係を理解しよう!』です!
この仕事とエネルギーの関係を理解できるかどうかは、冒頭でもお伝えしたように、高校物理の分野は力学、波動、熱力学、電磁気学、原子の5分野のうち、力学、熱力学、電磁気学、原子の4分野でずーっと重要になります!
なので、是非理解していきましょう!!
仕事とエネルギーのイメージ方法!
まずは、『仕事のイメージができない』という人のために、仕事とエネルギーをこのようにイメージしてみてください!
正の仕事のイメージ ⇒ お金を貯金するイメージ
負の仕事のイメージ ⇒ お金を浪費するイメージ
エネルギーのイメージ ⇒ お金とイメージする
慣れてくるとこんなことは考えなくてよくなるんですが、最初のときだけこのようにイメージしてみると勉強しやすくなります!(^^)!
仕事とエネルギーの関係を徹底理解!
では最後に仕事とエネルギーの関係を徹底理解してこの記事を終わりにしたいと思います!
ここでおさらいなのですが、仕事の定義は
定義①:仕事は力の距離的影響力を表す物理量
定義②:仕事はエネルギーを変化させる物理量
この2つでしたね!
この仕事とエネルギーの関係を理解するのには、『定義②』を意識してみましょう!
そうすると、定義②から、
<div class=”concept-box1″><p>(物体に$W$の仕事をする)=(物体が$W$のエネルギーが蓄えられる)</p></div>
ということがわかりますね!
ちなみに、$W>0$ならエネルギーが増加し、$W<0$ならエネルギーは減少するということです。
ただ、この関係は実はこの記事の中ですでに何度か出てきていることなので、この記事を最初から読んでみると、いつの間にか理解できるようになってきていると思います!
また、これをさっきの『仕事とエネルギーイメージ方法』を使ってリンクさせてみると、
(問題)
水平面上で1000Jの運動エネルギーをもっていた物体にはたらく摩擦力が-200Jの仕事をする。このとき、物体が持っている運動エネルギーの値を求めよ。
(解答)
この問題で
最初もっていた運動エネルギーが1000J ⇒ 最初1000円のお金を持っていた
途中で-200Jの仕事をした ⇒ 途中で200円分お菓子を買った(浪費した)
と思ってみてください。
そうすると、後に持っている運動エネルギー(お金)はいくらになりますか?
それは800J(800円)になりますよね?
この800J(800円)はどのように導出したかというと、
1000J+(-200J)=800J
ですよね?
最初に持っていたエネルギー(お金)に、途中でした仕事(貯金or浪費)を足すと、後でもっているエネルギー(お金)になるんです。
これは途中の仕事がエネルギーの変化量となっていることに等しいんです。
まとめ

以上で、『【高校物理】仕事とエネルギーの違いや関係を徹底理解!』の説明を終わりにします。
この記事を見てくれた皆さんが仕事とエネルギーの分野がしっかりと理解できてくれたらうれしいです!
ただ、仕事とエネルギーの分野って、実はまだ
- 運動エネルギー
- 仕事と運動エネルギーの関係
- 位置エネルギー
- 力学的エネルギー保存則
- 仕事と力学的エネルギーの関係
があるので、その記事もこれから書いていきますので、この記事を読んでくれたみなさんはまずはしっかりとこの記事『仕事とエネルギーの関係』を理解しておいてください!
また、このブログでは、

などの、物理の分野以外にも参考書、問題集、大学受験の対策方法などもまとめていますので、是非見てみてくださいね!






