みなさんこんにちは!
大手予備校で物理を教えているフィズ丸です!
今回のテーマは『コンデンサー』です!(^^)!
ただ、この記事を読んでいる人の大半はコンデンサーが苦手だと思います!
というか受験生の大半はコンデンサーが苦手だよね。。。
そして、毎年受験生の質問を受けていると受験生がつまづいているところが見えてきます。
- コンデンサーに電荷が蓄えられるイメージができていない。
- 電位のイメージができていない。
- 回路の切り替えで何が起こっているかがわかっていない。
- コンデンサーの問題の解法がわかっていない。
この上の4点を理解できればコンデンサーの問題は得点源にできるので頑張って理解しましょう!
Contents
コンデンサー回路の電荷の流れのイメージ

まずは、コンデンサー回路の電荷の流れを理解しましょう!
電磁気になるとイメージができないという生徒が続出するので、ここではコンデンサーに電荷が蓄えられるイメージを説明していきます。
①はすべてのコンデンサーの問題の土台になるし、②の5パターンは入試頻出なので理解しておくとそのまま入試に出ちゃうので理解は必須!しっかり理解しよう!
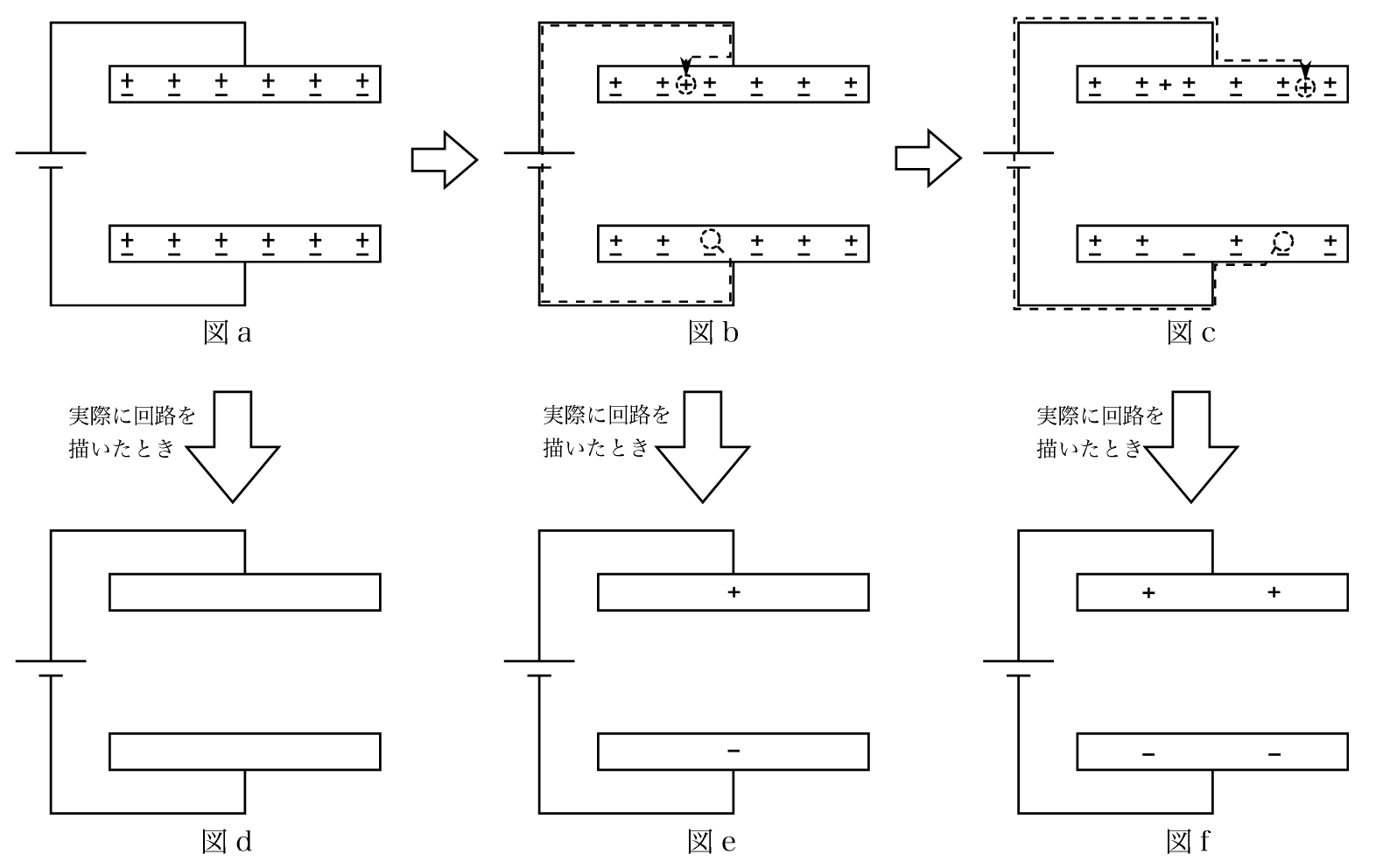
では『コンデンサーに電荷が蓄えられるイメージ』ですが、上の図aの状態がコンデンサーに電池を接続した瞬間だと思ってください。
このときにコンデンサーに使われている極板には+と-の数が同数入っていて、電気的に中性な状態です。
そして図aから図b、図cの順に回路に電流が流れるので、下の極板から導線を通り⇒電池⇒上の極板へと正の電荷が移動します。
つまり、下の極板は正の電荷がなくなったので、負に帯電し、上の極板は正の電荷が流入してきたので、正に帯電するということだね!
そして、実際に回路を自分で描くときは図d~fのように描くようにしましょう!
このように、コンデンサーに電荷が急に現れるのではなく、電荷が移動しているイメージが持てるとGoodです!
コンデンサーの問題はこの2種類のみ!

受験生の人はあまり意識していないですが、コンデンサーの問題は次の2種類に分けられます。
- 極板に着目した問題
- 回路に着目した問題
このどちらについても入試頻出なので、どんな問題なのかしっかりと理解しましょう!
極板に着目した問題
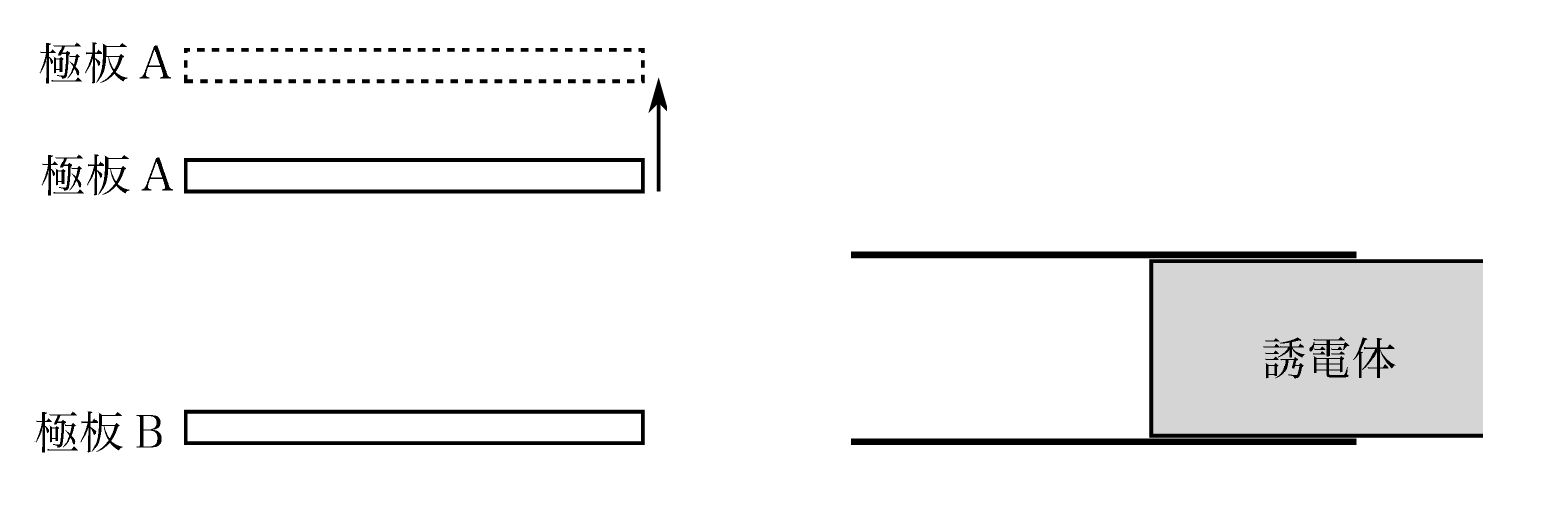
一つ目が『極板に着目した問題』です。
これは
- スイッチを閉じた状態で極板間隔を変える。
- スイッチを開いた状態で極板間隔を変える。
- スイッチを閉じた状態で誘電体を極板間に挿入する。
- スイッチを開いた状態で誘電体を極板間に挿入する。
など、回路全体に着目するよりもコンデンサー単体に着目する問題です。
特に、この問題のときに極板間の電場や極板間の電圧を求めさせることが特徴で、受験生を悩ませる問題だね!
回路に着目した問題
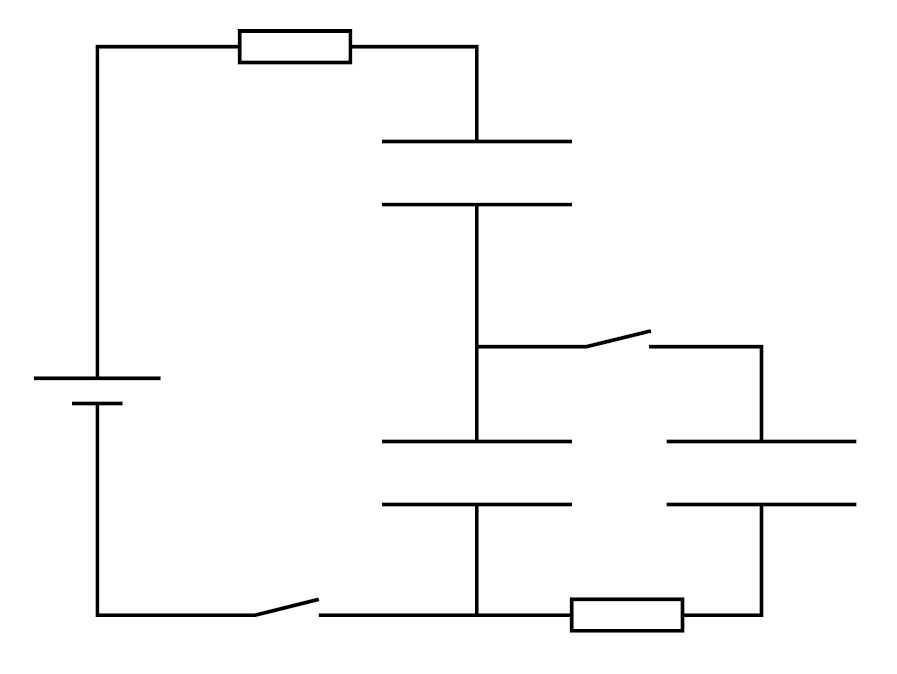
次は『回路に着目した問題』です。
この問題は上図のようにスイッチを切り替えて各状態の電気量やジュール熱を求めさせることが多いです。
そして、回路に着目した問題はさまざまな解法があるので、生徒の解法が定まらずに苦手になってしまう傾向が強いです。
回路に着目した問題は解法を1つ身に着けることに集中しよう!
極板に着目した問題の解法

では初めに『極板に着目した問題』の解法を説明します。
ここでは
- コンデンサーで使える公式を理解する。
- 解法を理解する。
の流れで説明するので、しっかりと理解しましょう!
使う式はこの4つ
コンデンサーの極板に着目した問題で使う公式
①:$C=\Large{\varepsilon \frac{S}{d}}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\Large{\frac{S}{d}}$
②:$Q=CV$
③:$E=\Large{\frac{\varepsilon S}{Q}}=\Large{\frac{\varepsilon_{\mathrm{r}}\varepsilon_{0}S}{Q}}$
④:$V=Ed$
極板に着目した問題で使うメイン公式はこの4つです。
一つずつ説明していくと、
①:コンデンサーの電気容量の公式です。極板間隔を変えたり、誘電体を挿入したときに使います。
②:コンデンサーの基本式です。
③:平行板コンデンサーの極板間の電場を表す式です。この式を覚えていない生徒がかなり多いのでしっかりと覚えておきましょう!
④:平行板コンデンサーの極板間の電場と極板間電圧の関係式です。
使う式を整理できている受験生は多くないので、しっかりと整理してどの式を使うかを判断できるようにしよう!
極板に着目した問題の解法
では次にここのメインテーマの『極板に着目した問題の解法』を説明していきます。
《極板に着目した問題の解法》
Step1:$C=\Large{\varepsilon \frac{S}{d}}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\Large{\frac{S}{d}}$を用いて電気容量を求めよう。
Step2:スイッチが開いているのか、閉じているのかを確認しよう。
<パターン①>スイッチが開いたままの変化
⇒電気量$Q$が一定。
<パターン②>スイッチが閉じたまま
⇒極板間電圧$V$が一定。
Step3:極板間の電場を求める。
<パターン①>スイッチが開いたままの変化
⇒電気量$Q$が一定なので$E=\Large{\frac{\varepsilon S}{Q}}=\Large{\frac{\varepsilon_{\mathrm{r}}\varepsilon_{0}S}{Q}}$を用いる。
<パターン②>スイッチが閉じたまま
⇒極板間電圧$V$が一定なので$V=Ed$を用いる。
この解法を下にある具体例で完全に身に着けましょう!
極板に着目した問題の具体例でみてみよう!!

では上で説明した解法を参考に具体例を4つ見てみましょう!
今から紹介する4つの具体例は、入試問題の基礎になるので、しっかりと理解して解けるようになろう!
具体例1:スイッチを開いて極板間隔を変える
《問題》

図1のように極板間隔$d$、電気容量$C_{0}$のコンデンサーに起電力$V$の電池を接続し、十分時間がたったとする。その後、スイッチを開き(図2)、極板間隔を$d$から$2d$に広げた(図3)。次の問いに答えよ。
(1)図3において、コンデンサーの電気容量$C_{1}$を$C_{0}$を用いて求めよ。
(2)図3において、コンデンサーに蓄えられる電気量$Q_{1}$を$C_{0}$、$V$を用いて求めよ。
(3)図3において、コンデンサーの極板間電圧$V_{1}$を$V$を用いて求めよ。
(4)図3において、コンデンサーの極板間電場$E_{1}$を$V$、$d$を用いて求めよ。
《解答》

図2の極板間電圧は電池の起電力に等しい。また、極板の面積を$S$、真空の誘電率を$\varepsilon_{0}$とすると、$$C_{0}=\varepsilon_{0}\frac{S}{d}$$となる。図2の電気量、電場をそれぞれ$Q_{0}$、$E_{0}$とすると、$$Q_{0}=C_{0}V$$ $$E_{0}=\frac{V}{d}=\frac{Q_{0}}{\varepsilon_{0}S}$$となる
(1)$C=\varepsilon \frac{S}{d}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\frac{S}{d}$より、$$C_{1}=\varepsilon_{0}\frac{S}{2d}=\underline{\frac{C_{0}}{2}}$$
(2)スイッチが開かれているので、コンデンサーに蓄えられた電気量は保存されるため、$Q_{0}$のままである。よって、$Q_{1}=Q_{0}=\underline{C_{0}V}$
(3)コンデンサーの電荷が$Q_{0}$で一定なので$Q=CV$を用いて、$$Q_{0}=C_{1}V_{1}=C_{0}V$$
$$\therefore V_{1}=\frac{C_{0}}{C_{1}}V=\underline{2V}$$となる。
(4)コンデンサーの電荷が$Q_{0}$で一定で、極板間の誘電率も$\varepsilon_{0}$で一定なので、$E=\frac{Q}{\varepsilon S}$より、電場$E_{1}$は$E_{0}$に等しい。よって、$$ E_{1}=E_{0}=\underline{\frac{V}{d}}$$
となる。
具体例2:スイッチを閉じて極板間隔を変える
《問題》

図1のように極板間隔$d$、電気容量$C_{0}$のコンデンサーに起電力$V$の電池を接続し、十分時間がたったとする。その後、図2のように極板間隔を$d$から$2d$に広げた。次の問いに答えよ。
(1)図2において、コンデンサーの電気容量$C_{2}$を$C_{0}$を用いて求めよ。
(2)図2において、コンデンサーに蓄えられる電気量$Q_{2}$を$C_{0}$、$V$を用いて求めよ。
(3)図2において、コンデンサーの極板間電圧$V_{2}$を$V$を用いて求めよ。
(4)図2において、コンデンサーの極板間電場$E_{2}$を$V$、$d$を用いて求めよ。
《解答》

図1の極板間電圧は電池の起電力に等しい。また、極板の面積を$S$、真空の誘電率を$\varepsilon_{0}$とすると、$$C_{0}=\varepsilon_{0}\frac{S}{d}$$となる。図1の電気量、電場をそれぞれ$Q_{0}$、$E_{0}$とすると、$$Q_{0}=C_{0}V$$ $$E_{0}=\frac{V}{d}=\frac{Q_{0}}{\varepsilon_{0}S}$$となる。
(1)$C=\varepsilon \frac{S}{d}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\frac{S}{d}$より、$$C_{2}=\varepsilon_{0}\frac{S}{2d}=\underline{\frac{C_{0}}{2}}$$
(2)スイッチが閉じているので、コンデンサーにかかる電圧は$V$で一定のままである。よって、$Q_{2}=C_{2}V_{2}=\underline{\frac{1}{2}C_{0}}V$
(3)スイッチが閉じたままなので、コンデンサーの極板間の電圧は変化しない。よって、$$V_{2}=\underline{V}$$となる。
(4)コンデンサーの極板間電圧が$V$で変化しないので、$V=Ed$を用いると、$$E_{2}=\underline{\frac{V}{2d}}$$となる。
【(4)の別解】
$E=\frac{\varepsilon_{0}S}{Q}$より$$E_{2}=\frac{Q_{2}}{\varepsilon_{0}S}$$となるので、$Q_{2}$と$C_{0}=\varepsilon_{0} \frac{S}{d}$を用いて、$$ E_{2}=\frac{\frac{1}{2}C_{0}V}{C_{0}d}=\underline{\frac{V}{2d}}$$とすることもできる。
具体例3:スイッチを開いて極板間に誘電体を挿入する
《問題》

図1のように極板間隔$d$、電気容量$C_{0}$のコンデンサーに起電力$V$の電池を接続し、十分時間がたったとする。その後、スイッチを開き(図2)、極板間に比誘電率が$\varepsilon_{\mathrm{r}}$の誘電体を満たした(図3)。次の問いに答えよ。
(1)図3において、コンデンサーの電気容量$ C_{3}$を$C_{0}$を用いて求めよ。
(2)図3において、コンデンサーに蓄えられる電気量$Q_{3}$を$C_{0}$、$V$を用いて求めよ。
(3)図3において、コンデンサーの極板間電圧$V_{3}$を$V$を用いて求めよ。
(4)図3において、コンデンサーの極板間電場$E_{3}$を$V$、$d$を用いて求めよ。
《解答》

図2の極板間電圧は電池の起電力に等しい。また、極板の面積を$S$、真空の誘電率を$\varepsilon_{0}$とすると、$$C_{0}=\varepsilon_{0}\frac{S}{d}$$となる。図2の電気量、電場をそれぞれ$Q_{0}$、$E_{0}$とすると、$$Q_{0}=C_{0}V$$ $$E_{0}=\frac{V}{d}=\frac{Q_{0}}{\varepsilon_{0}S}$$となる
(1)$C=\varepsilon \frac{S}{d}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\frac{S}{d}$より、$$C_{3}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\frac{S}{d}=\underline{\varepsilon_{\mathrm{r}}C_{0}}$$
(2)スイッチが開かれているので、コンデンサーに蓄えられた電気量は保存されるため、$Q_{0}$のままである。よって、$Q_{3}=Q_{0}=\underline{C_{0}V}$
(3)コンデンサーの電荷が$Q_{0}$で一定なので$Q=CV$を用いて、$$Q_{0}= C_{3}V_{3}=C_{0}V$$ $$\therefore V_{3}=\frac{C_{0}}{ C_{3}}V=\underline{\frac{V}{\varepsilon_{\mathrm{r}}}}$$となる。
(4)コンデンサーの電荷が$Q_{0}$で一定で、極板間の誘電率は$\varepsilon_{\mathrm{r}}\varepsilon_{0}$となるので、$E=\frac{Q}{\varepsilon S}$より、$$ E_{3}=\frac{\varepsilon_{\mathrm{r} }\varepsilon_{0} S}{Q_{0}}=\frac{E_{0}}{\varepsilon_{\mathrm{r}}}=\underline{\frac{V}{\varepsilon_{\mathrm{r}} d}}$$
となる。
具体例4:スイッチを閉じて極板間に誘電体を挿入する
《問題》

図1のように極板間隔$d$、電気容量$C_{0}$のコンデンサーに起電力$V$の電池を接続し、十分時間がたったとする。その後、極板間に比誘電率が$\varepsilon_{\mathrm{r}}$の誘電体を満たした(図3)。次の問いに答えよ。
(1)図2において、コンデンサーの電気容量$C_{4}$を$C_{0}$を用いて求めよ。
(2)図2において、コンデンサーに蓄えられる電気量$Q_{4}$を$C_{0}$、$V$を用いて求めよ。
(3)図2において、コンデンサーの極板間電圧$V_{4}$を$V$を用いて求めよ。
(4)図2において、コンデンサーの極板間電場$E_{4}$を$V$、$d$を用いて求めよ。
《解答》

図1の極板間電圧は電池の起電力に等しい。また、極板の面積を$S$、真空の誘電率を$\varepsilon_{0}$とすると、$$C_{0}=\varepsilon_{0}\frac{S}{d}$$となる。図1の電気量、電場をそれぞれ$Q_{0}$、$E_{0}$とすると、$$Q_{0}=C_{0}V$$ $$E_{0}=\frac{V}{d}=\frac{Q_{0}}{\varepsilon_{0}S}$$となる。
(1)$C=\varepsilon \frac{S}{d}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\frac{S}{d}$より、$$C_{4}=\varepsilon_{\mathrm{r}}\varepsilon_{0}\frac{S}{d}=\underline{\varepsilon_{\mathrm{r}}C_{0}}$$
(2)スイッチが閉じているので、コンデンサーにかかる電圧は$V$で一定のままである。よって、$Q_{4}=C_{4}V_{4}=\underline{\varepsilon_{\mathrm{r}} C_{0}V}$
(3)スイッチが閉じたままなので、コンデンサーの極板間の電圧は変化しない。よって、$$V_{4}=\underline{V}$$となる。
(4)コンデンサーの極板間電圧が$V$で変化しないので、$V=Ed$を用いると、$$E_{4}=\underline{\frac{V}{d}}$$となる。
【(4)の別解】
$E=\frac{\varepsilon_{0}S}{Q}$より$$E_{4}=\frac{Q_{4}}{\varepsilon_{\mathrm{r}} \varepsilon_{0}S}$$となるので、$Q_{4}$と$ C_{0}=\varepsilon_{0}\frac{S}{d}$を用いて、$$ E_{4}=\frac{\varepsilon_{\mathrm{r}} C_{0}V }{\varepsilon_{\mathrm{r}} C_{0}d}=\underline{\frac{V}{d}}$$として求めることもできる。
回路に着目した問題の解法

では次は『回路に着目した問題の解法』です!
この解法で必要な知識、習得して欲しい内容は
- キルヒホッフの第2法則
- 電気量保存則
の2つです!
なので、この2つを今から説明していきますね!
キルヒホッフの第2法則は電磁気分野すべてに絡んでくるので必ずできるようになろう!
キルヒホッフの第2法則
キルヒホッフの第2法則は回路における電圧の式になります。
ここでしっかりと回路のイメージを持っておく必要があるります。
《回路のイメージ》
回路を建物と考え、電圧は階を上がったり下がったりするイメージを持っておきましょう!
ではキルヒホッフの第2法則を説明していきます。
《キルヒホッフの第2法則》
着目した閉回路において(起電力の和)=(電圧の和)が成り立つ。
この式が成り立つのがキルヒホッフの第2法則です。
この後にキルヒホッフの第2法則の使い方を見ていくよ!
キルヒホッフの第2法則を使うときの2つの約束と使い方
上のキルヒホッフの第2法則の説明を受けて理解できる人はそもそもキルヒホッフの第2法則を知っている人です。
なので、次にキルヒホッフの第2法則の2つの約束と使い方を説明していきます。
ただ、キルヒホッフの第2法則の使い方は教える人によってさまざまなので、すでに習得している人はその方法で構いません!
まずは2つの約束です。
《約束①》電池の起電力は電圧が上がる向きを正とする。
《約束②》抵抗やコンデンサーは電圧が下がる向きを正とする。
では次に、キルヒホッフの第2法則の使い方です。
《使い方》
Step①:回路に電流をテキトーに設定する。
Step②:抵抗には①で決めた電流の向きに電圧の矢印を書き、コンデンサーには正電荷から負電荷の向きに電圧の矢印を書く。
Step③:①の閉回路を回る向きを決め、その向きと同じ向きの電池を正、逆向きん電池を負として左辺に起電力の和を書き、抵抗やコンデンサーも閉回路を回る向きに対して同じ電圧の矢印を正、逆向きを負として電圧の和を書く。
では次にこれをもとに具体例を2つほど見ていきましょう!
やることがたくさんあるように思えるけど、実際は慣れたら一瞬で立てられるようになるから、安心してね!
キルヒホッフの第2法則を具体例で練習してみよう!
では2つの具体例を確認してみましょう!
《具体例①》
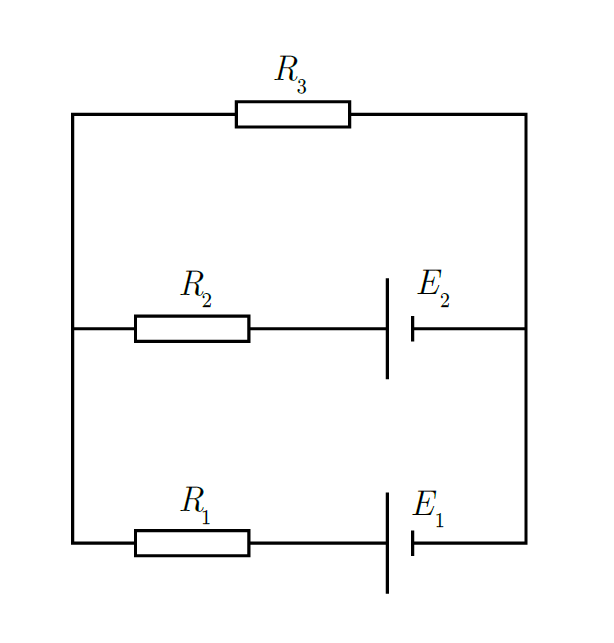
上図のように起電力が$E_{1}$と$E_{2}$の電池と抵抗値が$R_{1}$、$R_{2}$、$R_{3}$の抵抗を導線で接続した。このとき、各抵抗を流れる電流をStep①~③に沿って求めてみよう。
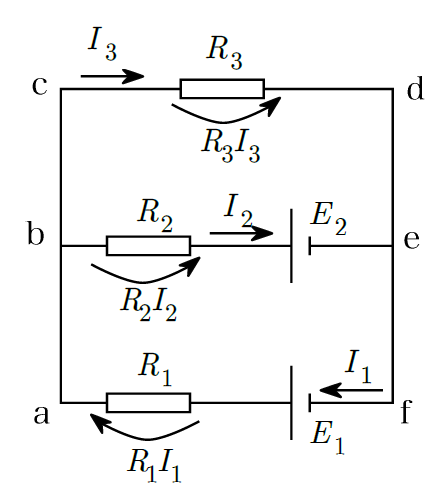
Step①:上図のように電流$I_{1}$~$I_{3}$をテキトーに設定します。本当にテキトーでいいです(笑)
Step②:抵抗にかかる電圧の矢印は、①で決めた電流の方向に設定する。
Step③:閉回路を決め、キルヒホッフの第2法則の式を立てる。
閉回路abefa:$+E_{1}-E_{2}=+R_{1}I_{1}+R_{2}I_{2}$
閉回路ebcde:$+E_{2}=-R_{2}I_{2}+R_{3}I_{3}$
閉回路acdfa:$+E_{1}=+R_{1}I_{1}+R_{3}I_{3}$
《具体例②》
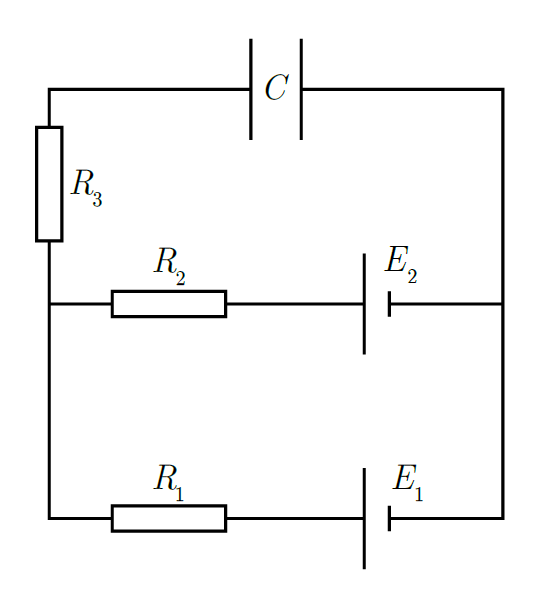
上図のように起電力が$E_{1}$と$E_{2}$の電池と抵抗値が$R_{1}$、$R_{2}$、$R_{3}$の抵抗、電気容量$C$のコンデンサーを導線で接続して十分時間がたった。このとき、各抵抗を流れる電流をStep①~③に沿って求めてみよう。
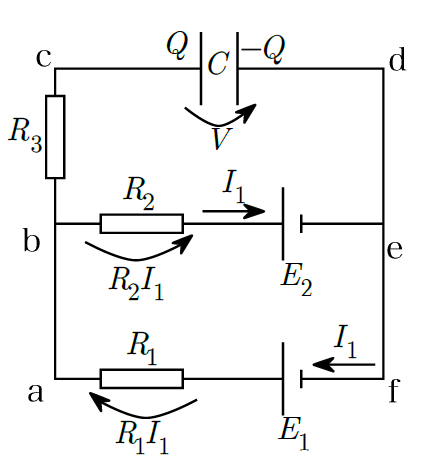
まず前提として、十分時間がたつとコンデンサーに電流は流れないので、$R_{3}$に流れる電流は0になります。
よって、電流が流れるのは閉回路abefaだけです。
Step①:上図のように電流$I_{1}$をテキトーに設定します。
Step②:抵抗にかかる電圧の矢印は、①で決めた電流の方向に設定する。また、コンデンサーには左側の極板に正電荷、右側の極板に負電荷が蓄えられるので、cからdの向きに電圧の矢印を書きます。
Step③:閉回路を決め、キルヒホッフの第2法則の式を立てる。
閉回路abefa:$+E_{1}-E_{2}=+R_{1}I_{1}+R_{2}I_{1}$
閉回路ebcde:$+E_{2}=-R_{2}I_{1}+V$
閉回路acdfa:$+E_{1}=+R_{1}I_{1}+V$
電気量保存則を使えるようになろう
では次に電気量保存則です!
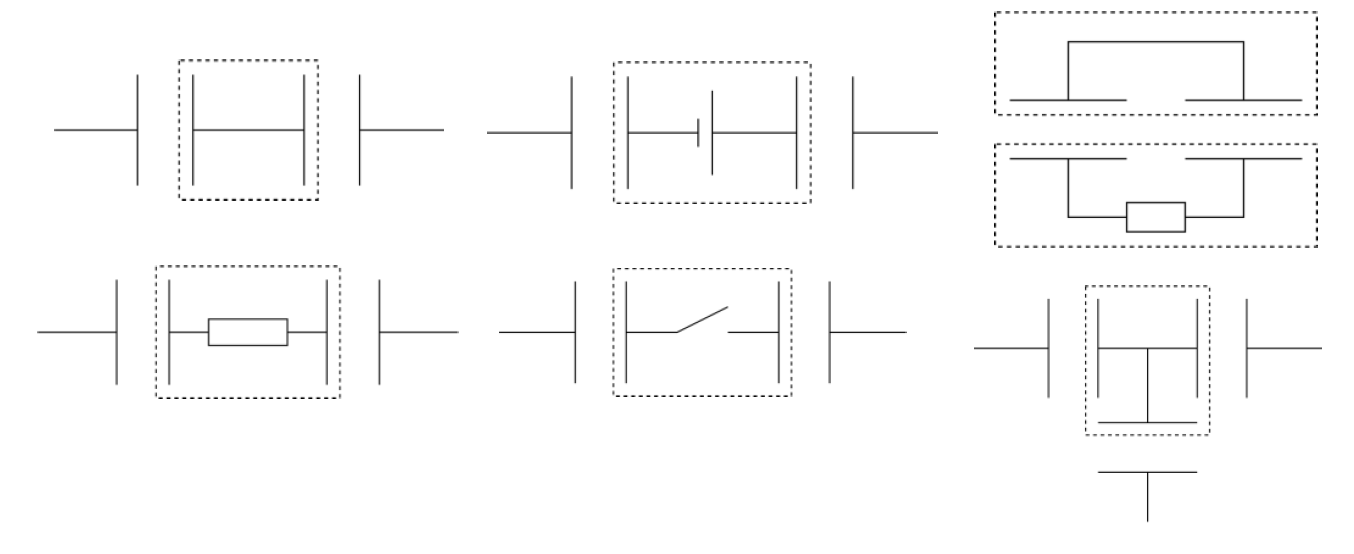
電気量保存則は上図のように回路の孤立部分(点線で囲まれた部分)に対して電気量が保存します。
電気量保存の使い方はこの後の具体例でしっかりと見ていくよ!
回路に着目した問題を具体例でみてみよう

では次に回路に着目した問題の具体例を見ていきます!
この回路の問題は電荷の流れをしっかりとイメージできるようにしておきましょう!
今から紹介する4つの具体例は、入試問題の基礎になるので、しっかりと理解して解けるようになろう!
具体例1:コンデンサー1個の場合

(Ⅰ):スイッチSを閉じた直後はコンデンサーの電荷は0なので、コンデンサーの電圧も0です。よって、回路には時計回りに、$$I_{0}=\frac{V}{R}$$となる電流が流れ、コンデンサーの上の極板に正電荷, 下の極板に負電荷が溜まり始めます。(このとき, コンデンサーの下の極板から正電荷が移動したので, 下の極板は負に帯電し, 上の極板には正電荷が回ってくるので, 正に帯電すると考えればいいです。)
(Ⅱ):コンデンサーに電荷が溜まってくると、コンデンサーの極板間に電圧が生じます。ただし、コンデンサーに蓄えられる電気量$q$が小さいとコンデンサーの極板間電圧$v$も小さいです。ここで、点Cを電位0とすると、点Aの電位は$V$、Bの電位は$v$となります。よって、抵抗$R$には$V-v(>0)$の電圧がかかるため、回路にはまだ電流が流れています。このとき、キルヒホッフの第2法則の式は, $$V=RI+v$$となることがわかりますね。
そして、時間がたつと$q$が大きくなり、$Q=CV(v=V)$になったときに、抵抗の電圧が0になり、回路に流れる電流が0(定常状態)になります。これが(Ⅲ)の図です。
具体例2:コンデンサー2個の直列接続

(Ⅰ):コンデンサー2つに蓄えられている電気量は0なので、抵抗には電池の起電力に等しい電圧がかかっています。よって、このとき回路には時計回りに$I_{0}=\frac{V}{R}$の電流が流れています。
(Ⅱ):正の電荷が時計回りに移動するので、それぞれのコンデンサーの上の極板に正電荷、下の極板に負電荷が蓄えられます。点Cの電位を0とすると、点Aの電位は$V$、点Bの電位は$v_{1}+v_{2}$となります。$q_{1}$や$q_{2}$の電気量が小さいとき、$v_{1}$や$v_{2}$も小さいため、$V> v_{1}+v_{2}$となります。よって、抵抗には電圧がかかるため、電流は流れるので、その電流をとすると、キルヒホッフの第2法則の式は$$V=RI+ v_{1}+v_{2}$$となります。
(Ⅲ):十分時間がたち、$V=V_{1}+V_{2}$が成り立つと、点Aと点Bが等電位となるため、回路に流れる電流が0になります(定常状態)。このとき、$$\mathrm{キルヒホッフの第2法則}:V=V_{1}+V_{2}・・・①$$ $$\mathrm{電気量保存則}:-Q_{1}+Q_{2}=0\leftrightarrow -C_{1}V_{1}+C_{2}V_{2}=0・・・②$$となるので、①、②式を連立すると$V_{1}$、$V_{2}$、$Q_{1}$、$Q_{2}$が求められる。
具体例3:コンデンサーの直列と並列接続がともにある

(Ⅰ):コンデンサーの電荷が0なので、抵抗にかかる電圧は電池の起電力に等しい。よって、このとき回路に流れる電流は$I_{0}=\frac{V}{R}$となります。
(Ⅱ):回路に電流(正電荷)が流れ、各コンデンサーの上側極板には正電荷が、下側極板には負電荷が蓄えられます。このとき、電気容量$C_{2}$と$C_{3}$のコンデンサーは同じ導線でつながれているので、電圧は等しいことに気付けるようにしましょう。よって、回路のキルヒホッフの第2法則の式は、$$V=RI+v_{1}+v_{2}$$となります。
(Ⅲ):十分時間がたち、$V=V_{1}+V_{2}$となると、抵抗の電圧が0になり、流れる電流が0になります。このとき、$$\mathrm{キルヒホッフの第2法則}:V=V_{1}+V_{2}・・・①$$ $$\mathrm{電気量保存則}:-Q_{1}+ Q_{2}+ Q_{3}=0 \leftrightarrow -C_{1}V_{1}+ C_{2}V_{2}+ C_{3}V_{3}=0・・・②$$の2式が成り立ち、①、②を解くと$V_{1}$、$V_{2}$、$Q_{1}$、$Q_{2}$、$Q_{3}$が求まります。
具体例4:コンデンサー2個の並列接続(電池なしver)

(Ⅰ):電気量$Q=CV_{1}$が蓄えられたコンデンサーを電気量0のコンデンサーに接続した直後は、$C_{1}$のコンデンサーの電圧$V$に等しい電圧が抵抗にかかるため、回路には時計回りに$I_{0}=\frac{V}{R}$の電流が流れる。
(Ⅱ):流れる電流の向きから、電気容量$C_{2}$のコンデンサーの上側極板に正電荷が蓄えられ、下側極板に負電荷が蓄えられる。ある時刻に、$q_{1}$の電気量が時計回りに移動したとする。$q_{1}$が小さいとき$v_{1}>v_{2}$となり、点Aの方が点Bより電位が高くなるので、回路に電流が流れる。
(Ⅲ):十分時間がたつと、$q_{1}$の値が大きくなり、$v_{1}=v_{2}=V´$となると抵抗の両端が等電位となり、回路に流れる電流が0になる(定常状態)。このとき、$$電気量保存則:Q_{1}+Q_{2}=Q$$ $$\leftrightarrow C_{1}V´+C_{2}V´=C_{1}V$$ $$\therefore V´=\frac{C_{1}}{C_{1}+C_{2}}V$$となります。
まとめ

以上で『【電磁気】コンデンサーの解き方はこれで決定!物理受験者必見!』の記事を終わりにします。
コンデンサーの分野は入試頻出ですので、しっかりとこの記事を読んで理解していきましょう!
特に、『極板に着目した問題』と『回路に着目した問題』の2つのパターンがあるので、その解法は定着させておく必要がありますね!
また、このサイトでは物理の分野解説以外にも名大や京大などの対策の記事も書いているので是非読んでください!








