どうも!大手予備校で物理を教えているフィズ丸です!
最初の物理の分野で放物運動でイメージできなくて物理が苦手になる
は物理初心者アルアルです!
放物軌道自体はイメージできるけど、問題を解くときになると急に手が止まるんですよね~。
なぜでしょうか?
私が10年以上物理を教えてきて、様々な生徒が質問にくる中で放物運動の問題で解けない理由は3点しかないことがわかりました!
放物運動の問題が解けない理由
- 放物運動の解法がわかっていない。
- 問題を解くときの運動のイメージがわかっていない。
- 問題演習量が足りていない。
の3点が挙げられます。
むしろこの3点の解決方法がわかれば放物運動はできるようになります!
なので、この記事ではこの3点について詳しく説明し、放物運動の問題を解けるようにしていきましょう!
ちなみに、物理をしっかりと理解するにはやはりプロに教えてもらうのは1番なので、プロ家庭教師を選べるサイトも紹介しておきますね!(^^)!
無料の体験授業もあるので、是非見てくださいね!!
Contents
【物理】放物運動の解き方は1つだけ!徹底解説!

では早速見ていきましょう!
①解法:鉛直方向と水平方向にわけて考える
まず①の解法ですが、これは放物運動の解法はこれ1択になります。
放物運動の解法はこの1つで決定!!
⇒ 鉛直方向と水平方向に運動を分解して考える。
この鉛直方向と水平方向に運動を分解して解く!ということを徹底していきましょう!
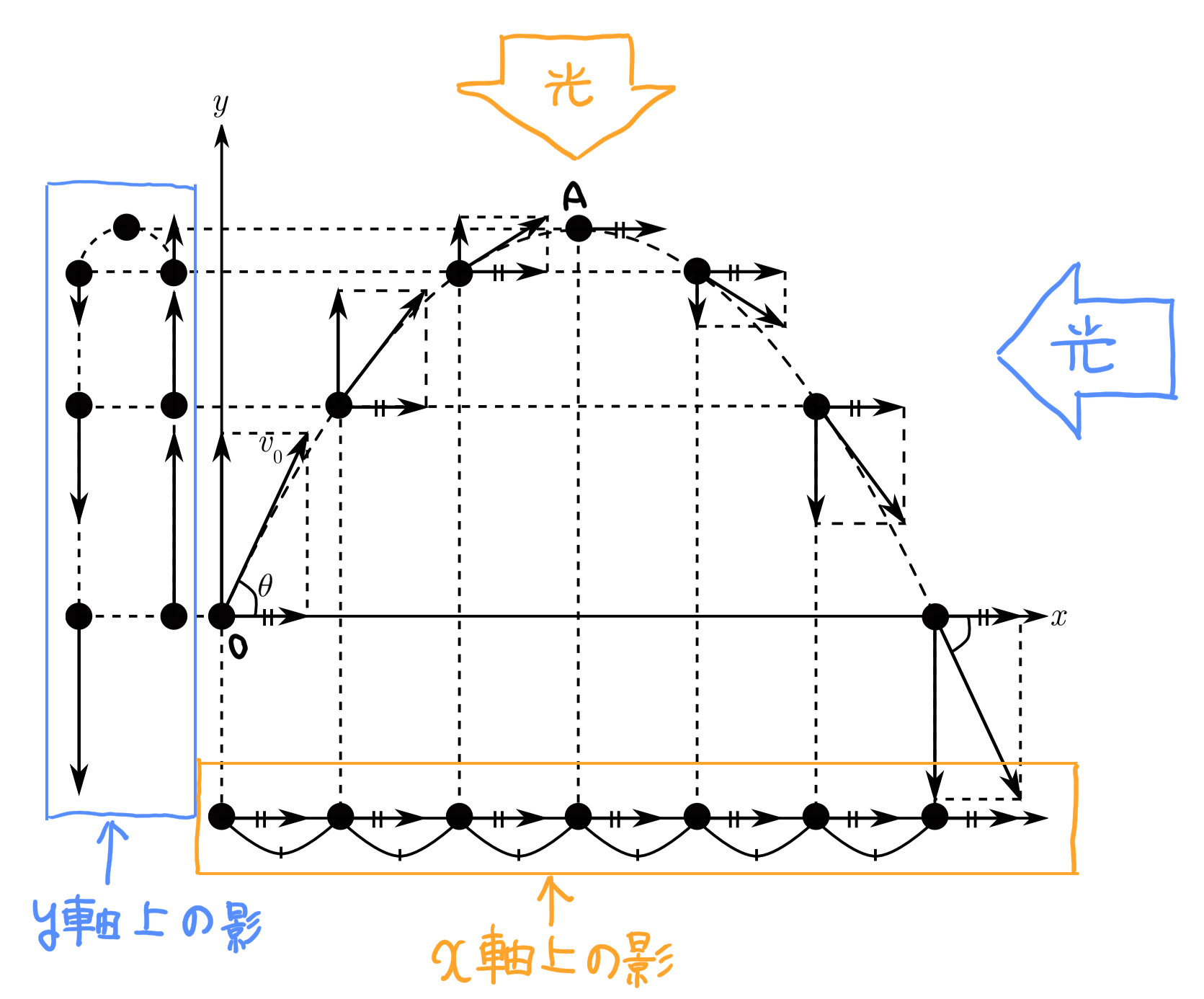
放物運動は上図のように山なりに運動するので、その運動を
- 鉛直方向($y$軸方向)
- 水平方向($x$軸方向)
に分けて一定の時間間隔の$x$軸上と$y$軸上の影を見てみます。
そうすると、上図のように$x$軸は等間隔の影が、$y$軸上は等間隔にならない影が現れます。
$x$方向が等間隔になるのは、$x$方向は加速度0なため、等加速度で運動するからです!
$y$方向が等間隔にならないのは、$y$方向には重力加速度があるからなんですね!
《鉛直方向($y$軸方向)》
初速度$v_{0}\sin\theta$、加速度$-g$の等加速度直線運動
《水平方向($x$軸方向)》
速さ$v_{0}\cos\theta$の等速直線運動
となることがわかりますね!
ただ、これがなかなか習得できないようで、解法はわかっていても解けない人が大勢います。
それが次の②注意点になるので、どんどん見ていきましょう!
②注意点:鉛直方向を考えているときは水平方向は無視する。水平方向を考えているときは鉛直方向は無視する。
『①解法』で話したことを理解したら放物運動の問題が解けるかと言ったら、実際そうじゃない生徒はかなり多いです。
それはなぜかというと、鉛直方向($y$軸方向)を考えなくてはならないのに、なぜか水平方向($x$軸方向)に動いていることを考えてしまっているからなんです!
またそういう生徒は、水平方向($x$軸方向)を考えなくてはならないときに、鉛直方向($y$軸方向)の運動も考えてしまっているんです。
これを解決するには、
《解決方法》
鉛直方向に着目しているときは、水平方向は無視した図を描く
水平方向に着目しているときは、鉛直方向は無視した図を描く
ということです。
物理で図示をすることはかなり重要で、図を描くことでそういうミスも解決できるようになります。
具体的には、『①解決方法』の放物軌道の図において、原点Oを飛び出して最高点に達するまでの時間$t_{\mathrm{ A }}$と、最高点の座標$(x_{\mathrm{ A }},y_{\mathrm{ A }})$を求めてみる。
まず、t_{\mathrm{ A }}とy_{\mathrm{ A }}を求めるために、鉛直方向に着目してみると、下図のようになります。
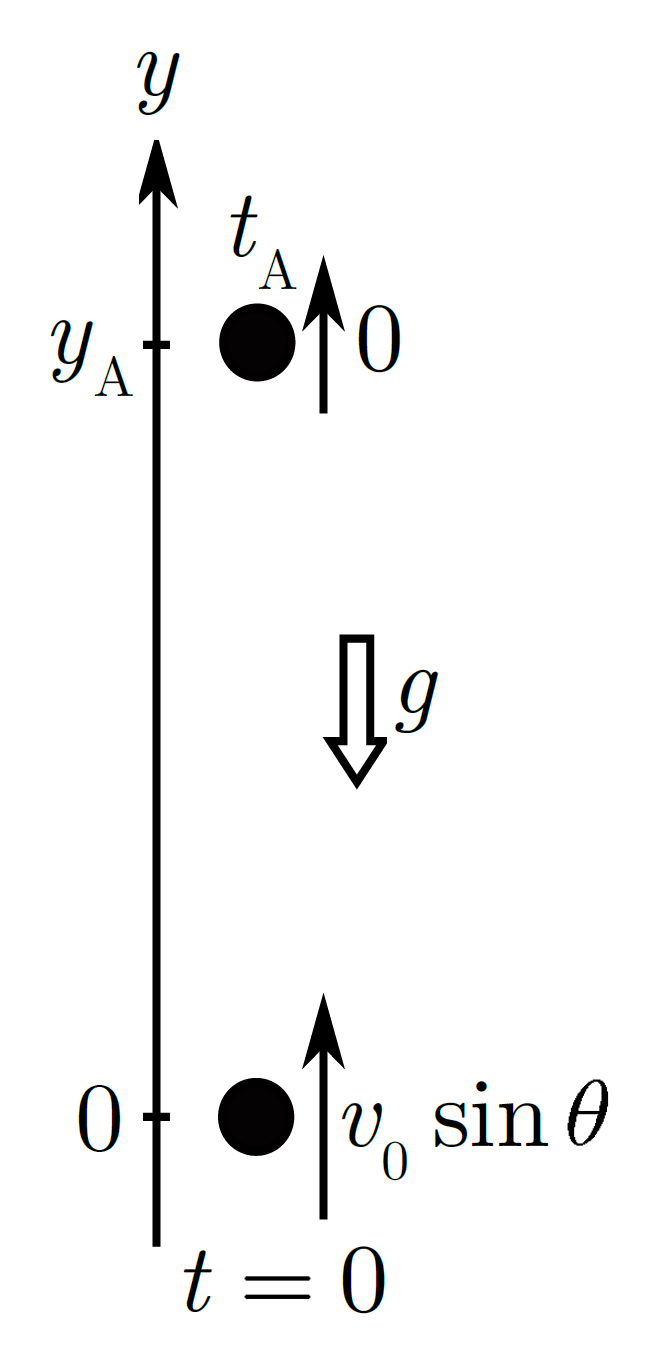
どうですか?この図には水平方向の成分は完全に無視されていますよね??
この図から$t_{\mathrm{ A }}$を求めるためには、等加速度直線運動の公式$v=v_{0}+at$を用いて$$0=v_{0}\sin\theta-gt_{\mathrm{ A }}$$この式から$$t_{\mathrm{ A }}=\frac{v_{0}\sin\theta}{g}$$となります。
また、$y$座標$y_{\mathrm{ A }}$は、等加速度直線運動の公式$v^{2}-v_{0}^{2}=2ax$を用いて、$$0-(v_{0}\sin\theta)^{2}=-2gy_{\mathrm{ A }}$$となるので、この式を変形して$$y_{\mathrm{ A }}=\frac{(v_{0}\sin\theta)^{2}}{2g}$$となる。
このように、鉛直方向に着目して問題を解くときは全く水平方向を無視して解けるんです!
また、$x$座標$x_{\mathrm{ A }}$を求めるために水平方向に着目します。
その図が下図になります。
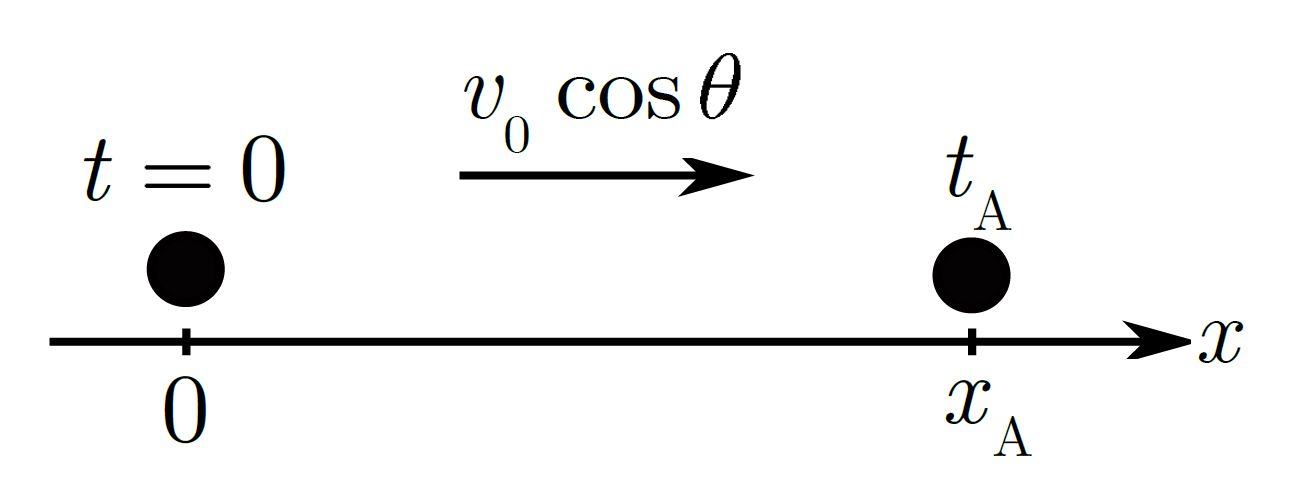
この図のように、水平方向に着目しているときは鉛直方向の成分は全くもって無視するんです!
そうすると、水平方向は等速直線運動なので$$x_{\mathrm{ A }}=v_{0}\cos\theta\times t_{\mathrm{ A }}$$にt_{\mathrm{ A }}を代入すると$$x_{\mathrm{ A }}=\frac{v_{0}^{2}\sin\theta\cos\theta}{g}$$となります。
どうですか??
再度確認ですが、
《解決方法》
鉛直方向に着目しているときは、水平方向は無視した図を描く
水平方向に着目しているときは、鉛直方向は無視した図を描く
これができれば1段階クリアですね!(^^)!
次は最終的にどうすれば問題が解けるようになるかの解決方法です!
③解決方法:問題演習をする
最後が『問題演習をする』になります!(^^)!
物理をできるようになるには
- 物理現象を理解する。
- 問題を何度も解きながら公式を覚える。
この2点をしっかりとこなすことです!
問題演習をするのに、基礎レベルをクリアしやすい問題集をまとめた記事をまとめてあるので是非見てくださいね!

また、物理現象を理解するために必要なのは参考書で、わかりやすい参考書をまとめた記事もあるので是非見てくださいね!

まとめ

以上で『【物理】放物運動の解き方は1つだけ!徹底解説!』を終わりにします!
放物運動ってなかなかイメージしにくかい分野ですが、今回の唯一の解法と注意点に注目しながら問題演習をしてみてください!(^^)!
また、冒頭でもお伝えしましたが、プロに教えてもらうことで激的にできるようになるので、プロを選べる家庭教師のサイト是非見てみてくださいね!
無料で体験授業もできます!