みなさん初めまして。大手予備校で物理を教えている「フィズ丸」です!
今回は物理基礎の一番初めに学ぶ「等加速度直線運動」の公式を導出していきます!
この記事を読んでもらっているということは
- 等加速度直線運動の意味が分からない。
- 等加速度直線運動の公式の使い方がわからない。
という人が多いと思いますが、物理って一見難しいようですけど、勉強のコツがわかれば案外難しくないんです!
ひとまずこの等加速度直線運動の記事を読んで、そのコツをつかんでください!
この記事を読むと
- 等加速度直線運動の意味がわかる。
- 等加速度直線運動の公式の使い方がわかる。
私は長年大手予備校や個別指導の予備校で教えている経験から、生徒が質問してくる内容はだいたい理解しています。
なので、その解決策としては
- 単語の定義を理解する。
- 公式の導出を理解する。
- 等加速度直線運動の公式の使い方を具体例から学ぶ。
これをしっかりと抑えれば大丈夫です!
この解決策は私が高校2年生のときに実際に物理ができるようになったきっかけの方法なので、是非参考にしてください!
Contents
【物理基礎】等加速度直線運動の公式の導出を解説!

それでは
- 単語の定義を理解する。
- 公式の導出を理解する。
- 等加速度直線運動の公式の使い方を具体例から学ぶ。
を一つずつ見ていきましょう!(^^)!
単語の定義を理解する
では最初にこの分野で出てくる言葉の定義を確認していきましょう!
物理は言葉の定義を理解することがとても大事なので、どの分野でも最初に理解するようにしてみてください!(^^)!
- 「変化量」=「(変化後の量)ー(変化前の量)」
- 「変位」=「位置の変化量」=「(後の位置)ー(前の位置)」
- 「速度」=「単位時間あたりの変位」
- 「速さ」=「速度の大きさ」
- 「加速度」=「単位時間当たりの速度の変化量」
です。この単語は物理では基本中の基本なので、かならず理解して覚えましょう!
ただ、この定義を読んで理解できている人は多分この記事を読んでいないので(笑)
まずこの定義の②~④を具体例からちゃんと理解しておきましょう!
変位と距離、速度と速さの具体例
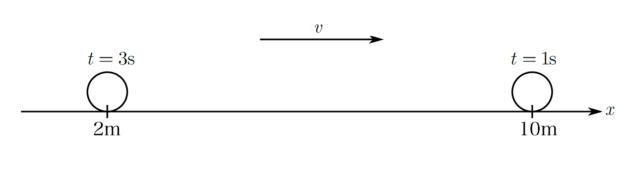
上図のように、$x$軸上を一定の速度$v$で運動している小球が、時刻$t=1\mathrm{ s }$に位置$x=10\mathrm{ m }$の位置を通過し、その後時刻$t=3\mathrm{ s }$に位置$x=2\mathrm{ m }$の位置を通過したとする。このとき、$$(変位)=2-10=-8\mathrm{ m }$$$$(移動距離)=8\mathrm{ m }$$$$(速度)=\frac{-8}{3-1}=-4\mathrm{ m/s }$$$$(速さ)=|v|=8\mathrm{ m/s }$$
となります。
しっかりと定義を理解してくださいね!
公式の導出を理解する
では続いて公式の導出をしていきましょう!
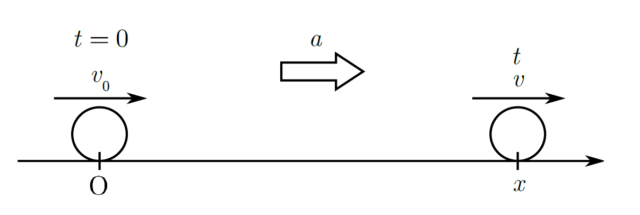
上図のように、一定の加速度$a$で運動している物体が、$x$軸上の原点Oを時刻$t=0$に初速度$\mathrm{\mathit{ v } }_0$で通過し、時刻$t$に位置$x$を速度$v$で通過したとする。
$v=v_{0}+at$の導出
この公式の証明には加速度の定義を用います。おさらいしておきましょう!
加速度の定義:単位時間当たりの速度の変化量
この定義を上図に用いてみると$$a=\frac{v-v_{0}}{t}$$となります。
なので、この式を変形すると、$$v=v_{0}+at・・・①$$が証明されます。
$x=v_{0}t+\frac{1}{2}at^{ 2 }$の導出
この式の証明には$v-t$グラフを用いて証明します。
簡単のため、$a>0$、$v_{0}>0$として①式を$v-t$グラフに表してみると、下図のようになる。
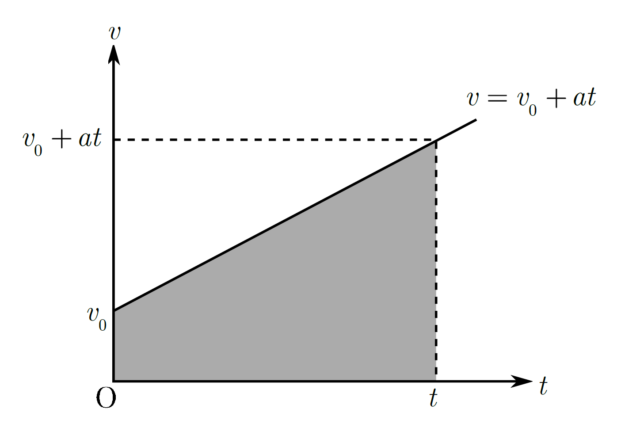
$v-t$グラフの面積は移動距離を表すので、上の$v-t$グラフの灰色部分の面積が$x$を表します。台形の面積公式より、
$$x=\frac{(v_{0}+v_{0}+at)t}{2}$$
よって、この式を変形して
$$x=v_{0}t+\frac{1}{2}at^{2}・・・②$$
となり、導出できました。
$v^{2}-v_{0}^{2}=2ax$の導出
最後の式を証明していきましょう。
①式と②式から時刻$t$を消去していく
①式より$t=\frac{v-v_{0}}{a}$となるので、この式を②式に代入すると
$$x=v_{0}\frac{v-v_{0}}{a}+\frac{1}{2}a(\frac{v-v_{0}}{a})^{2} $$
となるので、この式を変形して、
$$v^{2}-v_{0}^{2}=2ax・・・③$$
となり、導出できました。
この公式の導出を理解すると、等加速度直線運動の公式を深く理解することにつながるので、しっかりと理解していきましょう!
公式のまとめ
では導出した公式をまとめてみましょう。
$$v=v_{0}+at・・・①$$
$$x=v_{0}t+\frac{1}{2}at^{2}・・・②$$
$$v^{2}-v_{0}^{2}=2ax・・・③$$
この公式に用いられている文字の定義は、
$v$、$v_{0}$:速度(速さではない)
$x$:変位(距離ではない)
$t$:加速時間(時刻ではない)
となります。この定義はかなり重要になるので、次の具体例を見て、さらに理解を深めていきましょう!
具体例
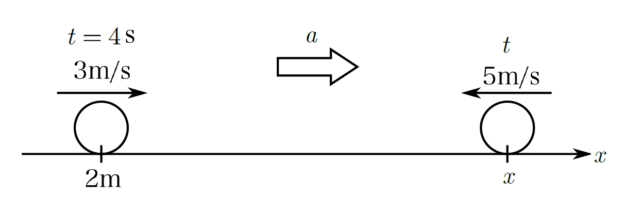
上図のように、一定の加速度$a$で運動している物体が、$x$軸上の原点Oを時刻$t=2\mathrm{ s }$に速さ$3\mathrm{ m/s }$で通過し、時刻$t$に位置$x$を$x$軸負の方向に速さ$5\mathrm{ m/s }$で通過したとする。
このとき、等加速度直線運動の3つの公式を立ててみましょう!
①$v=v_{0}+at$ ⇒ $-5=3+a(t-4)$
②$x=v_{0}t+\frac{1}{2}at^{2}$ ⇒ $x-2=3(t-4)+\frac{1}{2}a(t-4)^{2}$
③$v^{2}-v_{0}^{2}=2ax$ ⇒ $(-5)^{2}-3^{2}=2a(x-2)$
どうですか??$x$や$t$の代入がなかなか難しくないですか?
でもこの具体例を何度もやっておけば使い方はばっちりなので、自分の持っている問題集でどんどん演習をしてみましょう!
まとめ

これで「【物理基礎】等加速度直線運動の公式の導出を解説!」を終わりにしますね!
この記事を何度も読んで、公式の導出を何度も書いてみたり、具体例を何度も解いてみたりしたあとに問題集を演習するとすごく力がつくので、是非試してみてください!
また、このサイトでは高校物理の記事や入試情報をたくさん作っていますので、是非見てみてくださいね!