こんにちは!
大手予備校で物理を楽しく教えているフィズ丸です!(^^)!
物理ってわかるとかなり楽しいんですけど、わからなかったら苦行ですよね(笑)
毎年高校の物理の授業で力学的エネルギーの分野を習った後に
位置エネルギーの意味が分からない。
位置エネルギーの証明を知りたい。
っていう生徒がかなり多数現れます!
これはすでに全国の高校物理を学んだ生徒の共通の疑問でしょうね!
なので、その疑問を晴らすべく選んだ今回のテーマは
位置エネルギーの公式を証明からしっかりと理解すること!
です!
位置エネルギーの公式証明からしっかり理解して物理を楽しくしていきましょう!!
ちなみに、運動エネルギーについてはまた別の記事で説明していきますね!(^^)!
Contents
エネルギー、保存力、仕事の求め方を理解しよう!

- エネルギーの定義を理解する。
- 保存力をちゃんと理解する。
- 仕事の求め方を理解する。
これをしっかりと自分のなかに落とし込むことで位置エネルギーがすっと理解できるようになるので、頑張って読んでいきましょう!
エネルギーの定義
最初は『エネルギーの定義』です。
エネルギーって何だと思いますか?
それがわからない人はまずは定義をしっかりと抑えておきましょう!
《エネルギーの定義》
仕事をする能力のことをエネルギーという。
まぁこれを読んでわかってもらえればそれほど簡単なことはないんですが。。。(笑)
これがどういうことかを具体的な数字を用いて説明してみると、
1000Jの仕事ができるということは1000Jのエネルギーをもっている。
ということなんです。
文字で置き換えると
($W$〔J〕の仕事ができる)=($W$〔J〕のエネルギーをもっている)
ということになりますね!
保存力の定義
次に『保存力』についてです。
この保存力はちゃんとわかっている生徒がかなりすくないです。
ややこしい説明になりますので、気合を入れて読んでいきましょう!!
そのためには保存力の定義をしっかりと理解する必要がありますね。
《保存力》
始点と終点の位置が決まれば、経路に寄らず仕事が一定になる力のことを保存力という。また、位置エネルギーを定義できる力。
です。
なので、できるだけわかりやすく、かみ砕いて説明します!
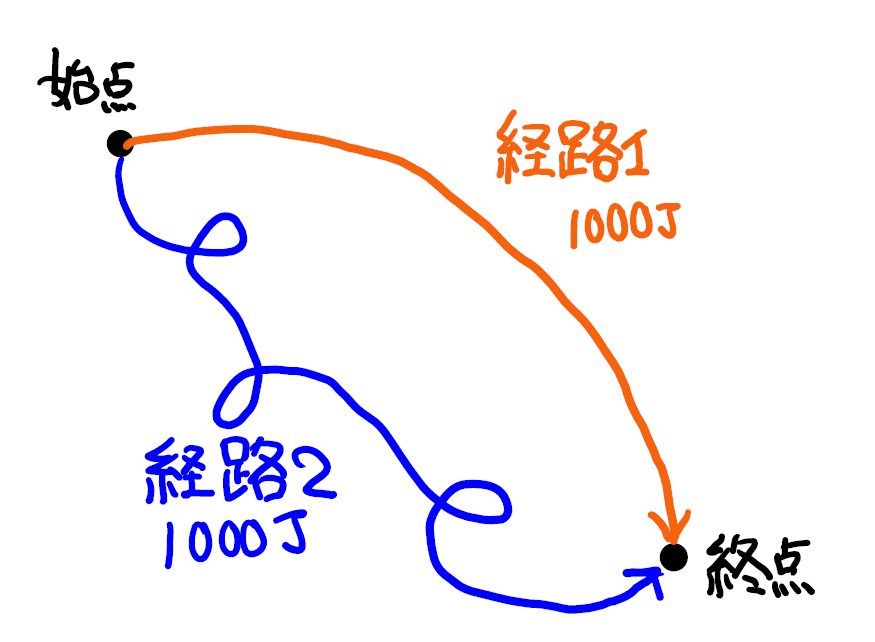
図のように、始点と終点の位置が決まっていて、物体が始点から終点の位置に2つの経路で移動していくことを考えてみましょう。
このとき、物体にはたらく保存力がする仕事はどの経路でも同じになります。(というか仕事が同じになる力を保存力と言います。)
なので『エネルギーの定義』でも話した通りですが、例えば
すべての経路でその力が1000Jの仕事で始点から終点に移動できるということは、終点から見るとその物体は始点で1000Jのエネルギーをもっているから。
ということになりますね!
だから、保存力は仕事がどんな経路でも等しいので位置エネルギーを定義できるんですね!
ちょっとはイメージつきましたか?
そして、高校物理で覚えておけばいい保存力は下の4つです!
《高校物理で出てくる保存力》
重力、弾性力、万有引力、静電気力(電場)
垂直抗力や張力などの他の力は保存力ではない力(非保存力)となります。
ここまでが位置エネルギーの意味の理解になります。
仕事の求め方
仕事の求め方は次の2Stepで求められます。
Step1:仕事の正負を判断しよう。
Step2:力が一定かどうかを判断し、
力が一定 ⇒ $W=Fx$を使う。
力が一定ではない ⇒ $W=$($F-x$グラフの面積)を使う。
詳しく仕事を学びたい人は、こちらの記事を読んでみてください!(^^)!

位置エネルギーの導出方法を理解しよう!

ここからは、始点と終点が決まればどんな経路でも仕事が一定になる4つ保存力によって定義される位置エネルギーを証明していきますね!
位置エネルギーの証明方法
まずは位置エネルギーの証明方法を確認しておきましょう!
保存力でもお伝えした通り、
物体にはたらく保存力が始点から終点に移動するときに1000Jの仕事をしたとすると、終点から見ると、その物体は始点で1000Jのエネルギーをもっているから
なんですね!
これめっちゃ重要ですね!
このことから、
《位置エネルギーの証明方法》
(位置エネルギー$U$)=(位置エネルギー0の位置に移動するまでに保存力がする仕事)
となることがわかりますね!
これめっちゃ重要ですね!!
ではこの証明方法を使って、力学で使われる
- 重力による位置エネルギー$mgh$
- 弾性力による位置エネルギー$\large{ \frac{1}{2} }kd^{2}$
- 万有引力による位置エネルギー$-G\large{ \frac{mM}{r} }$
の3つを証明していきましょう!
重力による位置エネルギー$mgh$の証明
1つ目は『重力による位置エネルギー$mgh$』です。
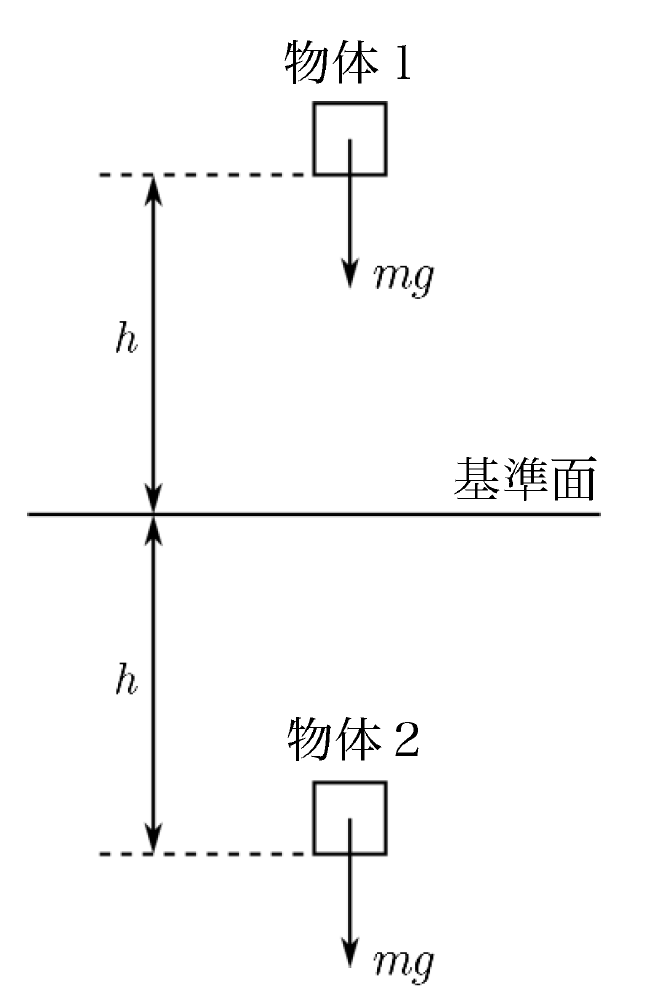
図のように、重力による位置エネルギーが0の場所(基準)から$h$高い場所と、$h$低い場所に質量$m$の物体を準備します。
このとき、重力による位置エネルギーはそれぞれの位置から基準の高さに移動するまでに、重力(保存力)がする仕事になります。
ではこの2物体の場合の重力による位置エネルギーをそれぞれ求めてみましょう!
まず、$h$高い場所にある物体にはたらく重力がする仕事は、『仕事の求め方』の2Stepより、
Step1:基準までに物体が移動する方向と保存力$mg$の向きは同じ向きなので正の仕事をする。
Step2:保存力$mg$は一定の力なので、$W=Fx$で仕事を求める。
この2点を考慮すると、保存力$mg$が基準の高さに移動するまでにする仕事(重力による位置エネルギー)$U_{\mathrm{g}}$は、
$U_{\mathrm{g}}=mg\times h$
となります。
これが重力による位置エネルギーですね!
また、$h$低い場所にある物体にはたらく重力がする仕事は、『仕事の求め方』の2Stepより、
Step1:基準までに物体が移動する方向と保存力$mg$の向きは逆向きなので負の仕事をする。
Step2:保存力$mg$は一定の力なので、$W=Fx$で仕事を求める。
この2点を考慮すると、保存力$mg$が基準の高さに移動するまでにする仕事(重力による位置エネルギー)$U_{\mathrm{g}}$は、
$U_{\mathrm{g}}=-mg\times h$
となります。
このことからもわかるように、重力による位置エネルギーは正の値と負の値があります!
これが重力による位置エネルギーの証明です!
弾性力による位置エネルギー$\large{ \frac{1}{2} }kd^{2}$の証明
次は『弾性力による位置エネルギー$\large{ \frac{1}{2} }kd^{2}$』の証明です!
これも重力による位置エネルギーと同様ですが、弾性力による位置エネルギーの基準(位置エネルギーが0)の場所は必ず自然長になります。
なので、ばねが自然長から$x$伸びた(あるいは縮んだ)状態から自然長にもどるまでに弾性力がする仕事が弾性力による位置エネルギーとなります。
ではばねの長さが自然長に戻るまでに弾性力がする仕事をばねが伸びている場合と縮んでいる場合で求めてみましょう!
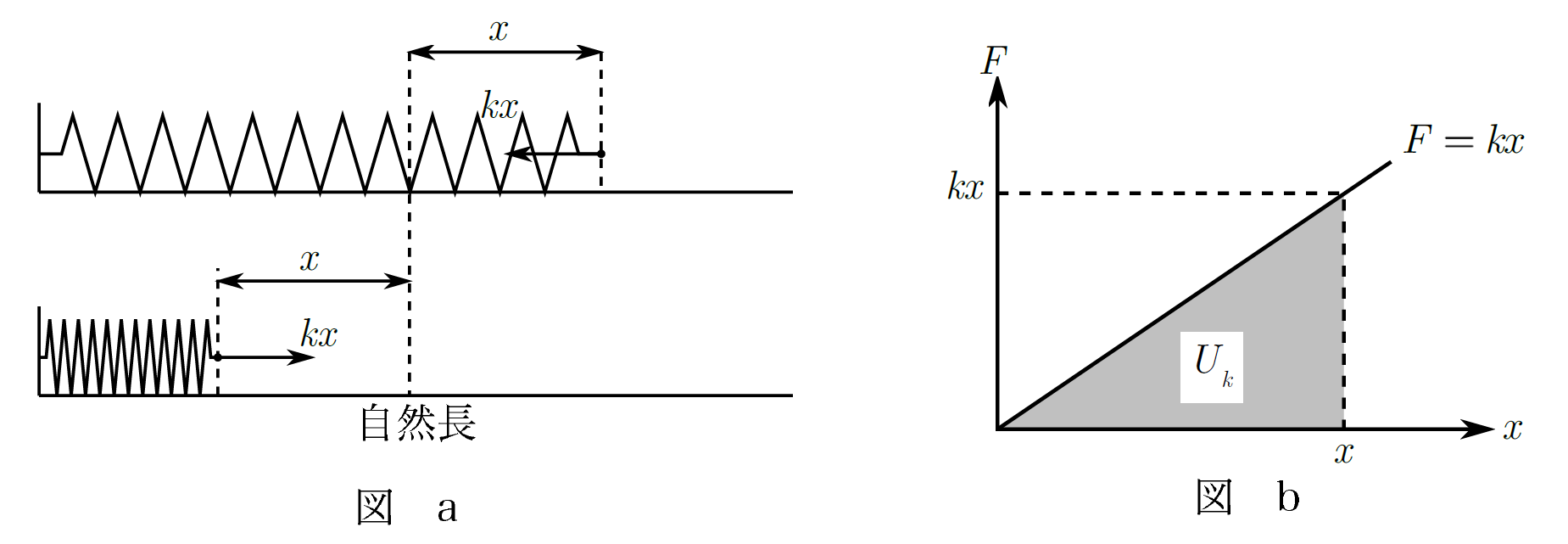
図aより、伸びている場合と縮んでいる場合の弾性力の仕事は、『仕事の求め方』の2Stepから求めていきましょう!
Step1:図aからばねが伸びている場合も縮んでいる場合も自然長までに戻る方向と保存力$kx$の向きは同じ向きなので、ともに正の仕事をする。
Step2:保存力$kx$は位置$x$に依存する一定でない力なので、図bの$F-x$グラフの面積から仕事の大きさを求める。
であることを考慮すると、自然長にもどるまでの$kx$の仕事(弾性力による位置エネルギー)$U_{\mathrm{k}}$は$F-x$グラフの面積を面積を用いて、
$U_{\mathrm{k}}=$$\large{ \frac{1}{2} }\times kx\times x$
となります。
これが弾性力による位置エネルギーの証明になります。
万有引力による位置エネルギー$-G\frac{mM}{r}$の証明
最後が『万有引力による位置エネルギー』の証明です!
学校ですでに万有引力の分野を学んだ人は是非読んで理解してください!
万有引力による位置エネルギーの基準(位置エネルギー0)の場所は無限遠方とすることがほとんどです。
なので、今回も無限遠方を基準として万有引力による位置エネルギーを証明していきますね!
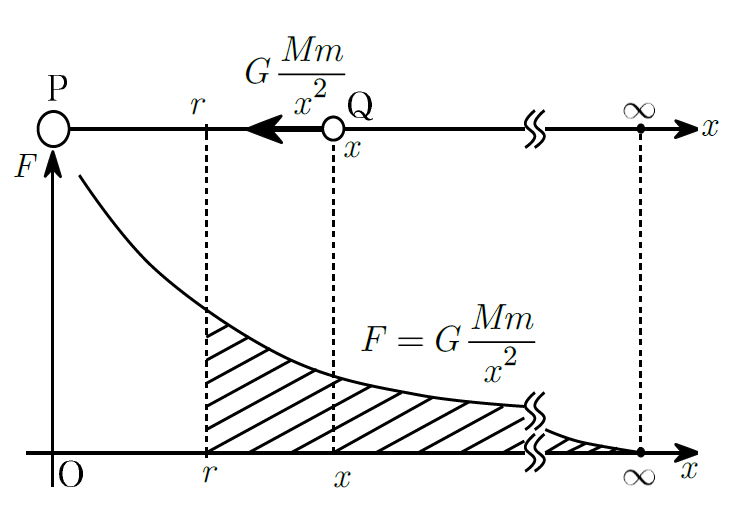
質量$M$の地球Pの中心を原点とした$x$軸を図のようにとります。
そして、位置$r$の場所から無限遠方まで質量$m$の衛星Qを移動させます。
このとき万有引力$-G\frac{mM}{r^{2}}$がする仕事が、位置$r$で衛星がもっている万有引力に位置エネルギーになるということですね。
では仕事を求める2Stepで確認していきましょう!
Step1:無限遠方に進む方向と保存力$G\frac{mM}{r^{2}}$の向きは逆向きなので、万有引力は負の仕事をする。
Step2:保存力$G\frac{mM}{r^{2}}$は位置$x$に依存する一定でない力なので、$F-x$グラフの面積が万有引力による位置エネルギーの大きさになる。
この2点を考慮すると、無限遠方に達するまでに万有引力がする仕事(万有引力による位置エネルギー)$U_{\mathrm{G}}$は$F-x$グラフの面積を面積を用いて、
$U_{\mathrm{G}}=$$-\displaystyle \int_{r}^{\infty} G\frac{mM}{r^{2}} dx$
となります!
これが万有引力による位置エネルギーの証明です!
まとめ

以上で『【高校物理】位置エネルギーの公式を証明からわかりやすく解説!』を終わりにします。
位置エネルギーはなかなかイメージしづらい分野なので、是非
- 保存力の理解
- エネルギーの定義
- 仕事の求め方
- 位置エネルギーの証明方法
の4点を意識してしっかりと理解してください!
また、このサイトではこの記事のような『物理現象の理解』や『物理の勉強法』など物理に関することを順次載せていくので、是非他の記事も読んでみてください!