こんにちは!
大手予備校で物理を楽しく教えているフィズ丸です!(^^)!
今回記事にしたのは物理基礎の力学で最大のテーマである『仕事と力学的エネルギー』の分野です!
- 力学的エネルギーの分野になると一気にイメージできなくなる
- そもそも式の立て方がわからない
- 力学的エネルギー保存則を使うタイミングがわからない
この上でまとめたような相談は毎年必ず出てきます!
なので今回のこの記事では上の疑問を取り除くために
- 仕事の定義を理解する。
- 運動エネルギーと位置エネルギーを理解する。
- 仕事と運動エネルギーの関係を理解する。
- 力学的エネルギーを理解する。
- 力学的エネルギー保存則が成り立つ状況と使い方を理解する。
- 仕事と力学的エネルギーの関係と使い方を理解する。
この6つの点について説明していきますね!
6つもあるの??って思う人もいるかもしれないのですが、1つ1つの理解が重要になるので根気強く何度も読んでみてください!
毎年何人も相談に来て、1つ1つ理解していくことでみんなできるようになっているので頑張っていこう!
この分野は【物理基礎】の力学で最後の砦を飾る分野でにありますが、何より
【物理】の力学や熱力学、電磁気学、原子分野でもガンガン使う分野
でもあります!
なので、
(仕事と力学的エネルギーの分野がわからない)≒(物理がわからない)
になってしまいかねないです。
そしてこの記事を読んでくれているみなさんの疑問や悩みを解消するために、みなさんがするべきことは
- ①~⑥をしっかり理解する。
- 問題演習を繰り返す 。
この2点だけです。
むしろ物理はこの2点ができれば誰でもできるようになる科目だよ!
なので、この2点を意識しながら勉強していきましょう!
Contents
仕事の理解

仕事についてですが、この仕事を理解するだけで1記事が書けるくらいの内容になるので、詳しく仕事を理解していきたい人は是非この記事を読んでみてください!

なので、ここでは仕事の定義と今回の記事を理解するうえで必要な部分だけ説明していきますね!
《仕事の定義》
- 仕事は力の距離的影響力を表す物理量。
- 仕事はエネルギーを変化させる物理量。
この2点は物理を学ぶ上でもかなり重要なので、しっかりと理解しておきましょう!!
そしてこの記事で必要な仕事の理解は②です!
②をもう少し今回の記事寄りの内容に落とし込むと
《今回使う仕事の考え方》
$W$の仕事をしたら$W$のエネルギーが変化する。
となります!
これをしっかりと理解しておきましょう!!
運動エネルギーを徹底理解!

さて、それでは最初に運動エネルギーを説明していきますね!
運動エネルギーは読んで字のごとく『運動しているときに物体が持っているエネルギー』です。
まずは運動エネルギーの公式を確認していきましょう!
運動エネルギーの公式
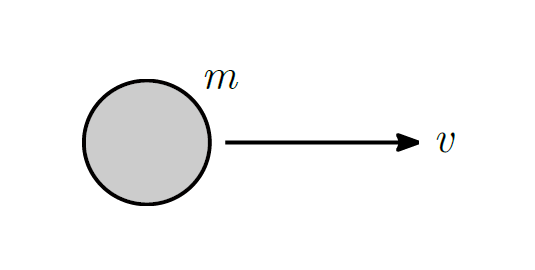
上図のように, 質量$m$の物体が速さ$v$で運動しているとき、この物体は$$\frac{1}{2}mv^{2}$$の運動エネルギーをもっています。
運動エネルギー$K$の公式 $K=\Large{\frac{1}{2}}$$mv^{2}$
これが運動エネルギーの公式です。
しっかりと覚えておきましょう!
運動エネルギーの導出
では続いて運動エネルギーの導出ですが、運動エネルギーの導出をする前に、エネルギーの定義を確認していきましょう!
エネルギーの定義
導出をする前に確認ですが、エネルギーとはなんでしたっけ??
これは
のところでみっちり説明してますので、エネルギーが何かわからない人はその記事も是非合わせて読んでみてください!
簡単に必要なところだけ説明してみると
エネルギーとは仕事をする能力のことです!
つまり1000Jの仕事ができるということは1000Jのエネルギーをもっているということでしたね!
これを逆に考えると、
物体に1000Jの仕事をした場合、物体には1000Jのエネルギーが蓄えられるということです。
この考えを使って運動エネルギーの導出をしてみます!
つまり、ちゃんと導出する方法を明確にしてみると
《運動エネルギー$K$の導出方法》
$K$=(物体を速さ0から$v$になるまでに外力が物体にした仕事)
このようになりますね!
運動エネルギーの導出
では導出していきます。
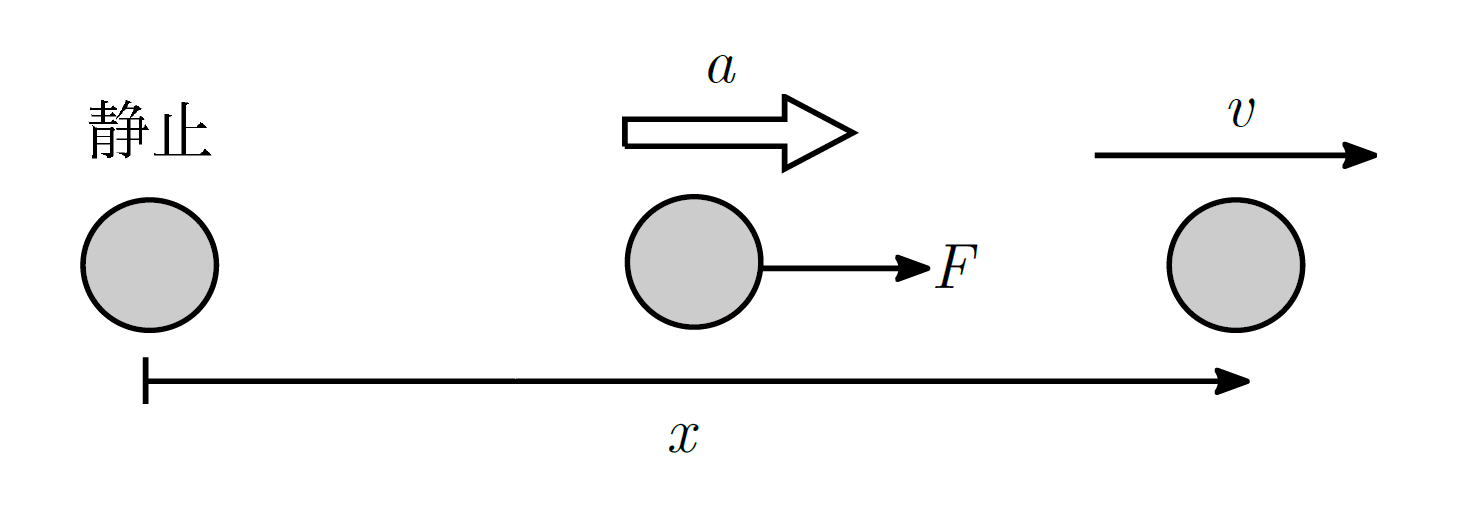
上図のように静止している質量$m$の物体に一定の大きさ$F$の外力を加え、水平方向に加速させます。
そして物体が距離$x$移動したときの速さを$v$とします。
このとき、外力がした仕事$W_{外}$は$F$が一定なので$W=Fx$より、$$W_{外} =Fx$$となります。
- 一定の力がした仕事の公式は$W=Fx$
- 一定でない場合の仕事は$W=(F-x$グラフの面積)
仕事を求めるときは基本的にこの2つだったね!
よって、この$W_{外}$が、外力が物体にした仕事であり、物体に蓄えられた運動エネルギーとなります。
ただし、運動エネルギーである以上この式を$v$で表す必要があるので、次にその作業に入ります。
この物体の加速度の大きさを$a$とすると、運動方程式より$$ma=F \hspace{15pt} \therefore a=\frac{F}{m} $$となります。
加速度$a$が一定の場合は等加速度直線運動の公式
- $v=v_{0}+at$
- $x=v_{0}t+frac{1}{2}at^{2}$
- $v^{2}-0^{2}=2\frac{F}{m}x$
の3つが使えるね!
よって、加速度$a$は一定なので、等加速度直線運動の公式$v^{2}-v_{0}^{2}=2ax$に代入してみると$$v^{2}-0^{2}=2\frac{F}{m}x$$となります。
以上から$$Fx=\frac{1}{2}mv^{2}$$となります。
$Fx$は外力がした仕事で、その仕事分運動エネルギーが蓄えられたので、これで運動エネルギーの導出完了です!
仕事と運動エネルギーの関係式を徹底理解!

では続いて『仕事と運動エネルギーの関係式』についてです。
まずここで再度確認しておきたいのは、仕事の定義です。
《仕事の定義》
①:仕事は力の距離的影響力を表す物理量。
②:仕事はエネルギーを変化させる物理量。
この2つでしたね!
今回使うのは2つ目の『仕事はエネルギーを変化させる物理量』です!
証明は微積を用いるので、ここでは省略しますが、使えればよい式は次の式になります。
《仕事と運動エネルギーの関係式》
(後の運動エネルギー)=(前の運動エネルギー)+(全ての力がした仕事の和)
単に覚えるだけでは理解力が乏しくなる一方なので、具体例からこの式が成り立つことを確認してみましょう!
具体例で仕事と運動エネルギーの関係式を導出
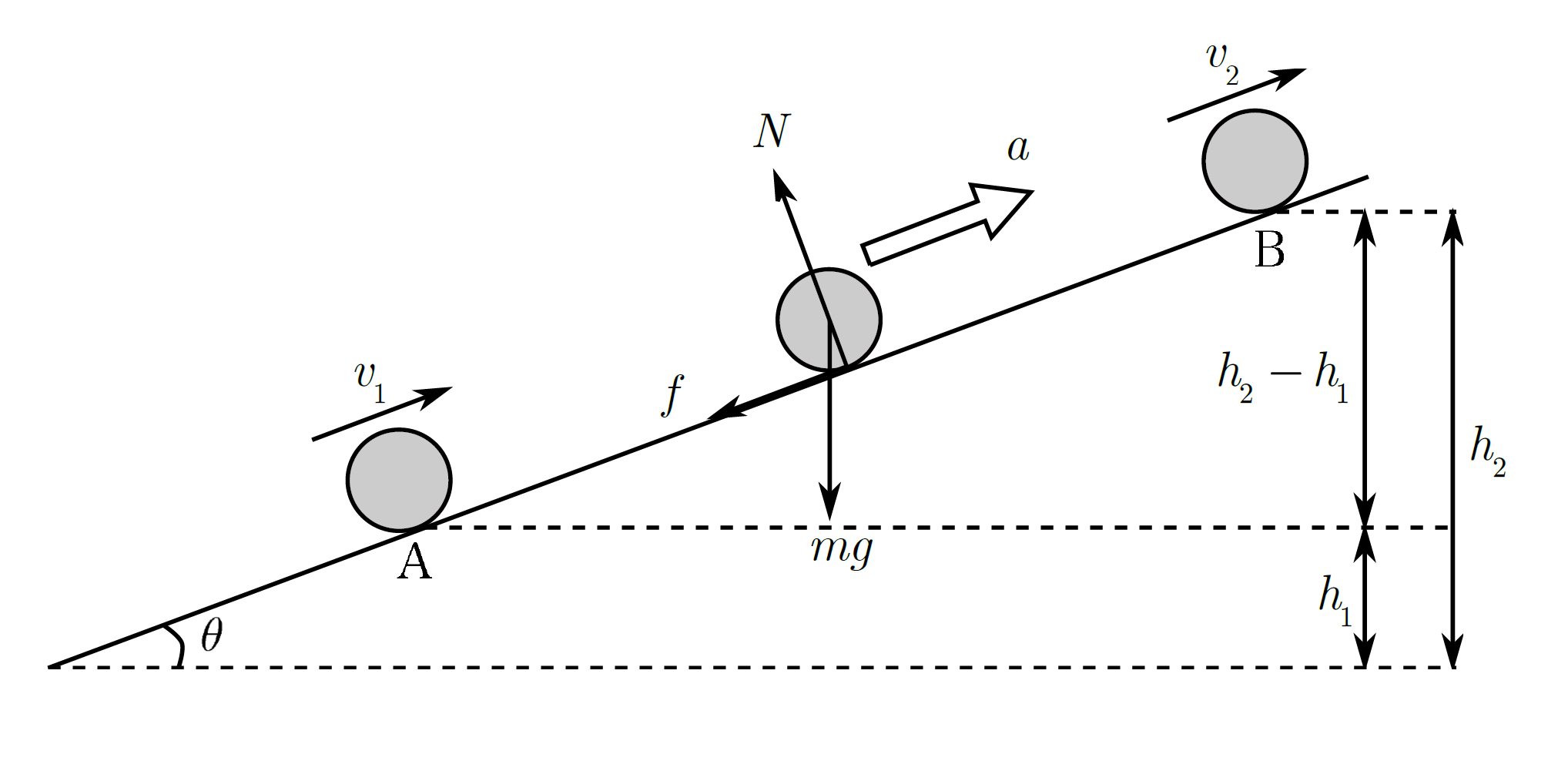
上図のように、あらい斜面上を基準面より高さ$h_{1}$の位置Aを質量$m$の小物体が速さ$v_{1}$で通過したとします。その後、重力$mg$と動摩擦力$f$、垂直抗力$N$を受けながら運動し、高さ$h_{2}$の位置Bを速さ$v_{2}$で通過した。ただし、AB間の距離を$l$とします。
さて、この具体例から仕事と運動エネルギーの関係を導いてみましょう!
Step1:位置AからBに移動するまでにすべての力がした仕事を求める。
Step2:運動方程式を立て$v^{2}-v_{0}^{2}=2ax$に代入する。
となりますので、この手順で導いてみましょう!
運動エネルギーの導出手順と同じだね!
Step1:位置AからBに移動するまでにすべての力がした仕事を求める
まず位置Aから位置Bに移動するまでに、小物体にはたらくすべての力がする仕事を求めてみます。
$mg$も$f$も$N$もすべて一定の力なので、$W=Fx$が使えるね!
重力がする仕事$W_{g}=-mg\sin\theta \times l =-mg \times (h_{2}-h_{1})$
動摩擦力がする仕事$W_{\mu}=-fl$
垂直抗力がする仕事$W_{\mathrm{N}}=0$
となりますね。
Step2:運動方程式を立て$v^{2}-v_{0}^{2}=2ax$に代入する。
次に、位置Aから位置Bに移動するまでの斜面上向きの加速度を$a$とすると、運動方程式は$$ma=-mgsin\theta -f$$となりますね。
よって、加速度$a$は$$a=-\frac{ mgsin\theta +f}{m}$$となります。
加速度$a$が一定であることがわかるね!つまり等加速度直線運動の公式が使えるね!
この加速度$a$は一定であるので、等加速度直線運動の公式$v^{2}-v_{0}^{2}=2ax$に代入してみると$$ v_{2}^{2}-v_{1}^{2}=2(-\frac{ mgsin\theta +f}{m})l $$
となるので、両辺に$\frac{1}{2}m$をかけてみると、$$\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}= -mglsin\theta -fl+0 $$
となることがわかりますね。つまり、$$\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}= W_{g}+ W_{\mu}+ W_{\mathrm{N}} $$
となりますね。
この式から、物体にはたらく全ての力がした仕事が運動エネルギーの変化量になっていることがわかると思います!
また、この式を少し変形すると、$$\frac{1}{2}mv_{2}^{2}=\frac{1}{2}mv_{1}^{2}+W_{g}+W_{\mu}+ W_{\mathrm{N}}・・・\mathrm{①} $$となるので、これが最初に紹介した『仕事と運動エネルギーの関係』です!
成り立つことが確認できましたね!
導出完了!この具体例でいいので、何度か手を動かしてノートや裏紙に書いてみるとかなり理解が深まるので、是非やってみてね!!
力学的エネルギーを徹底理解!

力学的エネルギーとは運動エネルギーと位置エネルギーの和のことを表します。
運動エネルギーは上で説明したので位置エネルギーを確認していき、その後、力学的エネルギーを見ていきましょう!
位置エネルギーを徹底理解!
位置エネルギーですが、これもがっつりまとめた記事がありますので、導出方法や意味などを詳しく知りたい方はこっちを参照ください!

なので、この記事では位置エネルギーの公式を3つほど軽くまとめておきます。
重力による位置エネルギー
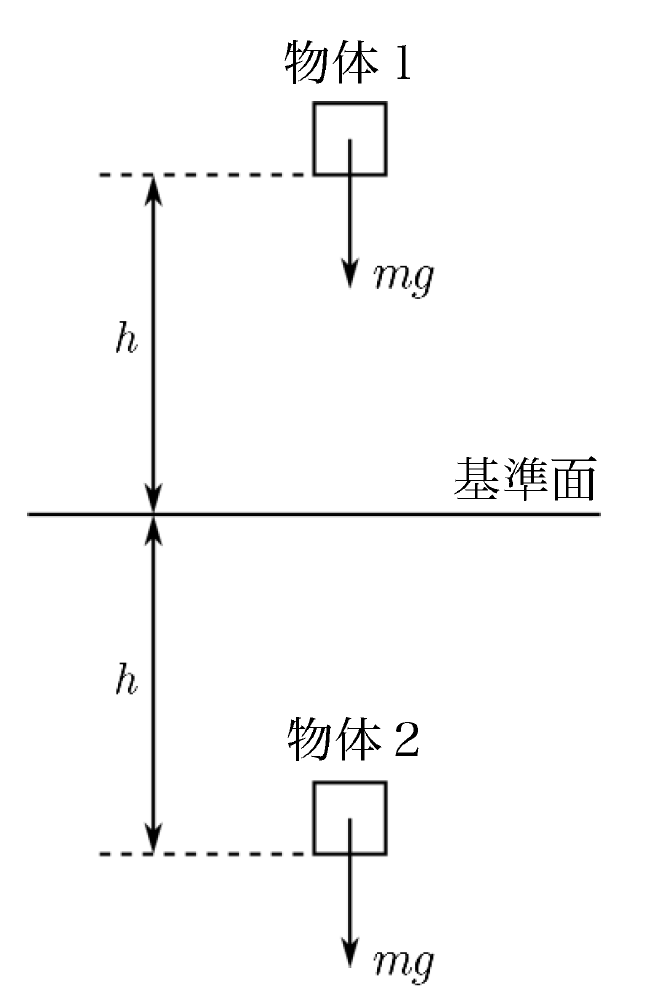
上図のように、質量$m$の物体が高さ0の基準から$h$高い場所にあると、その物体がもっている重力による位置エネルギー$ U_{g}$は$$U_{g}=mgh$$となります。
また、高さ0の基準から$h$低い場所にあると、その物体は重力による位置エネルギー$$U_{g}=-mgh$$をもっているということです。
重力による位置エネルギーは基準面よりも上ならプラス、下ならマイナスだね!
弾性力による位置エネルギー
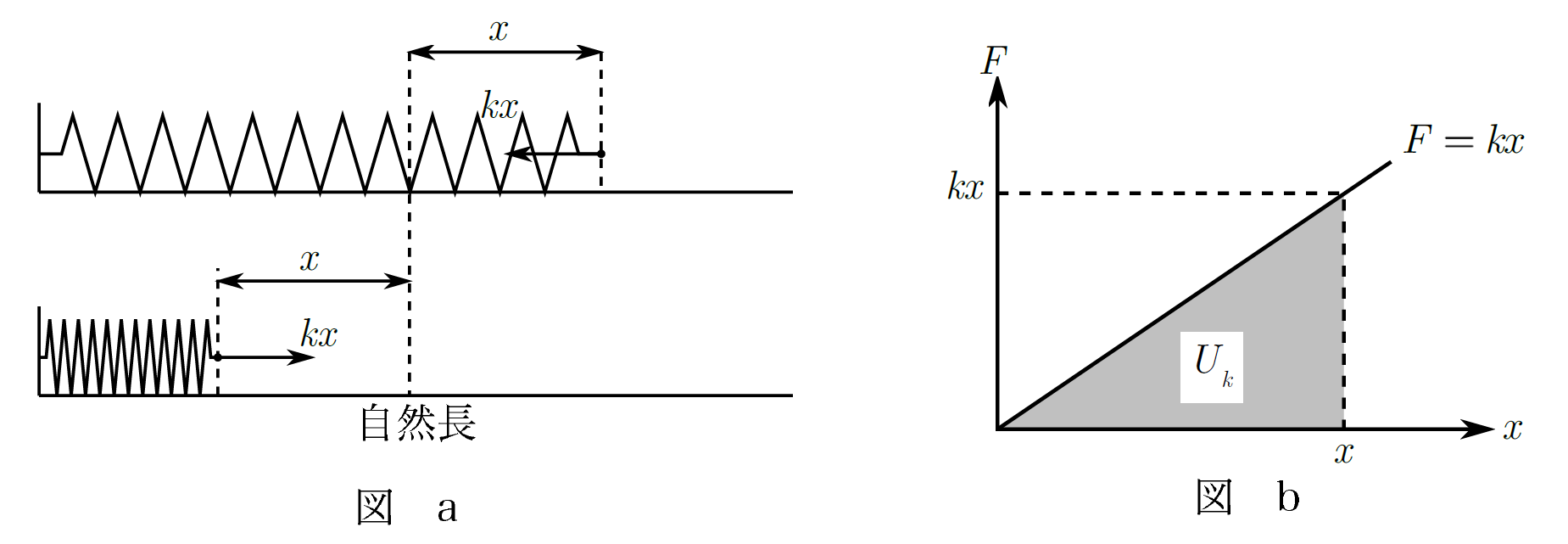
次は弾性力による位置エネルギーについてです。
図aのように、ばね定数$k$のばねが自然長から距離$x$だけ伸縮しているとき、ばねに蓄えられた弾性力による位置エネルギー$ U_{k}$は$$ U_{k}=\frac{1}{2}kx^{2}$$となります。
証明は図bの$F-x$グラフの面積を使うんだったね!
そして、弾性力による位置エネルギーはばねが縮んでも伸びても必ずプラスになるんだね!
力学的エネルギーを徹底理解!
力学的エネルギーは運動エネルギーと位置エネルギーの和とお伝えしました!
まずは具体例を用いて各時刻の力学的エネルギーを立式する練習をしてみましょう!
(例1)
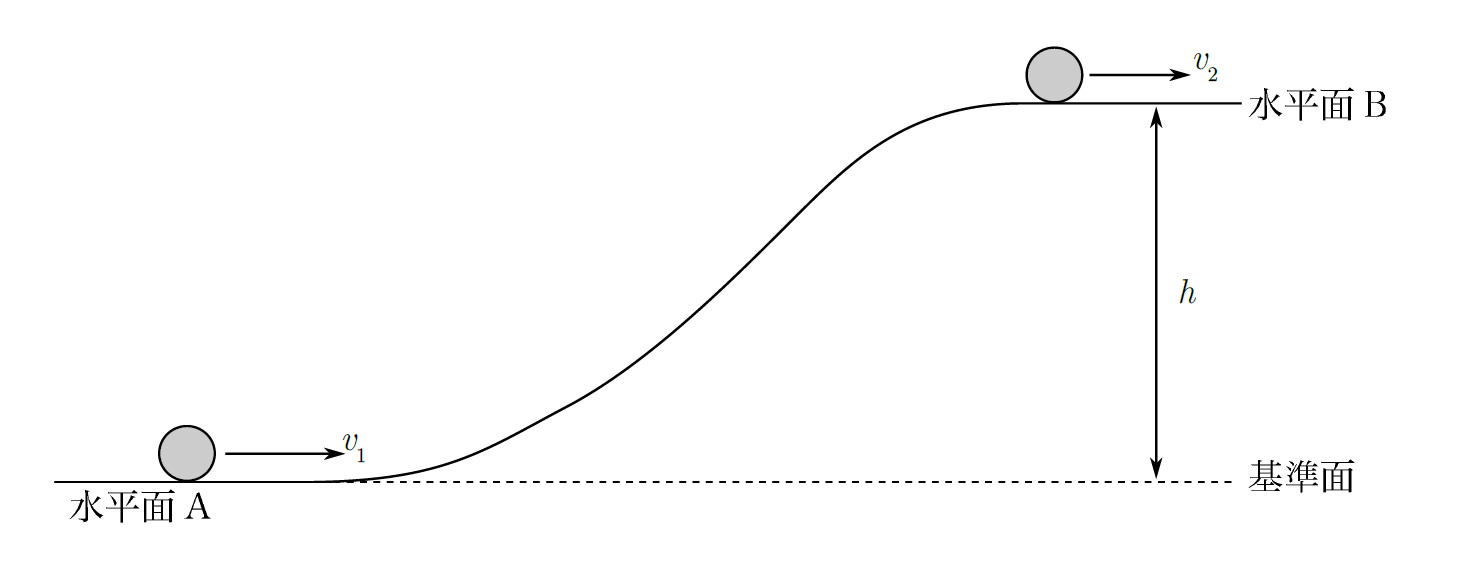
上図のように、高さが$h$だけことなる水平面Aと水平面Bがなめらかな曲面でつながっている。質量$m$の小球が水平面Aを速さ$v_{1}$で通過し、曲面を上って水平面Bを速さ$v_{2}$で運動した。このとき、水平面Aを高さの基準として水平面A上を運動しているときの小球の力学的エネルギー$E_{A}$と水平面B上を運動しているときの力学的エネルギー$E_{B}$を求めよ。
(解答)
水平面Aでは
- 運動エネルギー$K_{\mathrm{A}}=\Large{\frac{1}{2}}$$mv_{1}^{2}$
- 位置エネルギー$U_{\mathrm{A}}=mg \times 0 $
となるので、この2つの和が$E_{A}$であることから
$E_{A}=K_{\mathrm{A}}+U_{\mathrm{A}}=\Large{ \frac{1}{2}}$$mv^{2}$
水平面Bでは
- 運動エネルギー$K_{\mathrm{B}}=\Large{\frac{1}{2}}$$mv_{2}^{2}$
- 位置エネルギー$U_{\mathrm{B}}=mg \times 0 $
となるので、この2つの和が$E_{A}$であることから
$E_{B}=K_{\mathrm{B}}+U_{\mathrm{B}}=\Large{\frac{1}{2}}$$mv_{2}^{2}+mgh$
となります。
(例2)
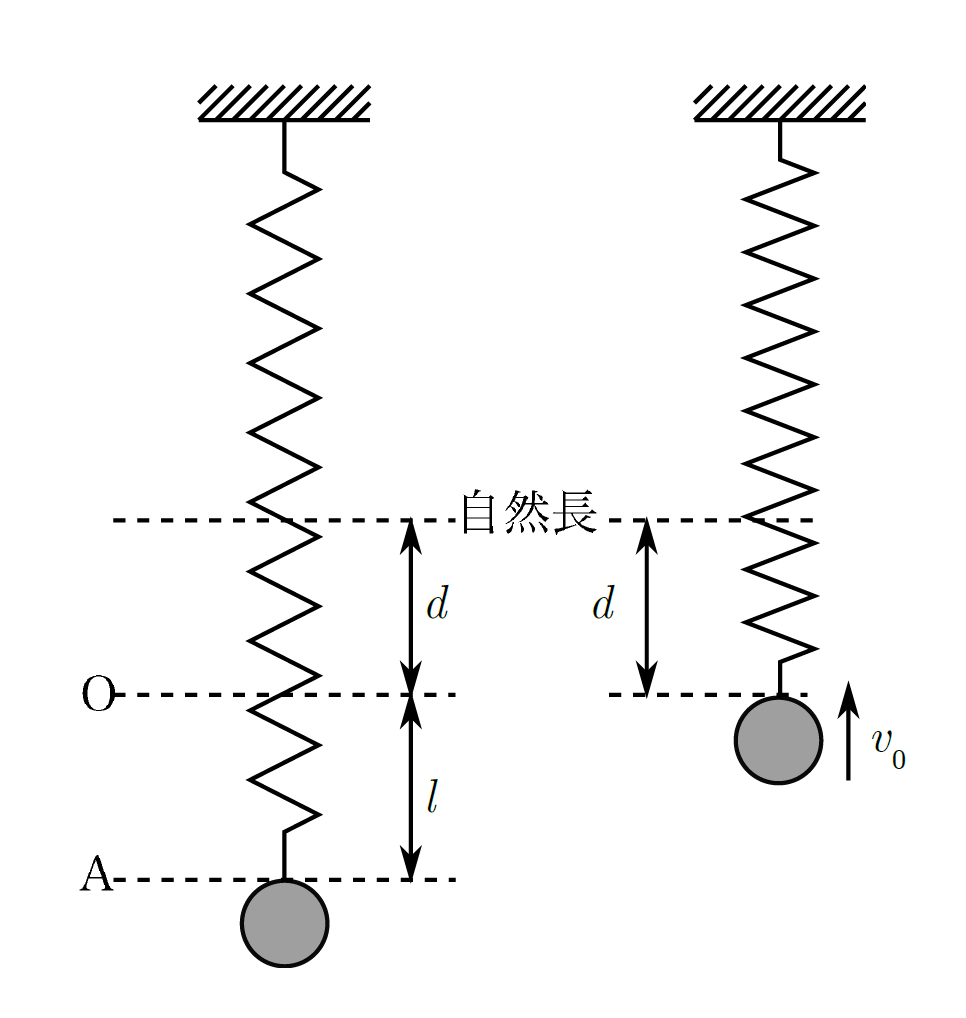
上図のように、ばね定数$k$のばねの一端を天井に固定し、他端に質量$m$の小球を取り付け吊るすと、ばねは自然長から$d$だけ伸びて静止した。この位置を点Oとする。点Oからさらに$l$だけばねを伸ばした点を点Aとし、点Aで静かに離す。小球が点Oを通過するときの速さを$v_{0}$、点Oを重力による位置エネルギーの基準として、点Aと点Oの力学的エネルギー$E_{A}$と$E_{O}$をそれぞれ求めよ。
(解答)
点Aでは
- 速さ0なので運動エネルギー$K_{\mathrm{A}}=0$です。
- 重力による位置エネルギーの基準から$d$だけ下がっているで、重力による位置エネルギー$U_{g\mathrm{A}}$は$U_{g\mathrm{A}}=-mgd$
- ばねは自然長から$d+l$だけ伸びているので、弾性力による位置エネルギー$U_{k\mathrm{A}}$は$\Large{\frac{1}{2}}$$k(d+l)^{2}$となります。
よって、$E_{\mathrm{A}}$は
$E_{\mathrm{A}}=K_{\mathrm{A}}+U_{g\mathrm{A}}+U_{k\mathrm{A}}=-mgl+\Large{\frac{1}{2}}$$k(d+l)^{2}$
重力による位置エネルギーと弾性力による位置エネルギーの2つあるので、2つとも考えないといけないね!
点Oでは
- 小球の速さは$v$なので、運動エネルギー$K_{0}$は$K_{0}=\Large{\frac{1}{2}}$$mv_{0}^{2}$となります。
- 点Oは基準面なので、重力による位置エネルギー$U_{g\mathrm{0}}$は$U_{g\mathrm{0}}=\mathrm{0}$となります。
- ばねは自然長から$d$だけ伸びているので弾性力による位置エネルギー$U_{k\mathrm{0}}$は$U_{k\mathrm{0}}=\Large{\frac{1}{2}}$$kd^{2}$となります。
よって、$E_{0}$は
$E_{0}=K_{0}+U_{g\mathrm{0}}+U_{k\mathrm{0}}=\Large{\frac{1}{2}}$$mv_{0}^{2}+\Large{\frac{1}{2}}$$kd^{2}$
となります。
どうでしょうか?力学的エネルギーの立て方わかりましたか??
この具体例ができればもう一歩!
運動エネルギーはわかりやすいけど、位置エネルギーの立式が練習が必要なので、しっかりとこの具体例で練習してね!
では続いては『仕事と力学的エネルギーの関係』と『力学的エネルギー保存則』を徹底理解していきましょう!
仕事と力学的エネルギーの関係式を徹底理解!

では続いて『仕事と力学的エネルギーの関係式』についてです。
ここでも『仕事はエネルギーを変化させる物理量』の考え方が重要になります!
証明は微積を用いるので、ここでは省略しますが、使えればよい式は次の式になります。
《仕事と力学的エネルギーの関係式》
(後の力学的エネルギー)=(前の力学的エネルギー)+(非保存力のした仕事の和)
※非保存力とは保存力以外の力のこと。つまり、重力、弾性力、万有引力、静電気力以外の力と思ってください。
上で説明した『仕事と運動エネルギーの関係式』と似てますよね?
実は『仕事と運動エネルギーの関係式』を少し変形すれば『仕事と力学的エネルギーの関係』が導けるんです。
それを確認していきましょう!
『具体例で仕事と運動エネルギーの関係を導出』の①式を変形していきましょう!
仕事と運動エネルギーの関係から仕事と力学的エネルギーの関係に変形
ではまず、①式の確認ですが、$$\frac{1}{2}mv_{2}^{2}=\frac{1}{2}mv_{1}^{2}+W_{g}+W_{\mu}+ W_{\mathrm{N}}・・・\mathrm{①} $$でしたね。
この式の仕事の部分を変形していくと、$$\frac{1}{2}mv_{2}^{2}=\frac{1}{2}mv_{1}^{2}+(-mgl\sin\theta -fl+0) $$となり、$mgl\sin\theta = mg(h_{2}-h_{1})$となることから$$\frac{1}{2}mv_{2}^{2}=\frac{1}{2}mv_{1}^{2}+(-mg(h_{2}-h_{1}) -fl+0) $$と変形できますね。
そしてこの式の重力がした仕事の項を分解して整理してみると$$\frac{1}{2}mv_{2}^{2}+mgh_{2}=\frac{1}{2}mv_{1}^{2}+mgh_{1}+(-fl+0) $$となることがわかりますね。
この式の左辺は後の力学的エネルギー、右辺の第1項と第2項の和が前の力学的エネルギーを表し、右辺の第3項以降が非保存力がした仕事の和になります。
これで導けましたね!
『仕事と運動エネルギーの関係』と『仕事と力学的エネルギーの関係』は実は同じ式!どっちもしっかりと使えるようにしておこう!
力学的エネルギー保存則が使える状況を徹底理解!
では力学的エネルギー保存則がつかる状況を徹底理解していきましょう!
でもこの理解はもうすでに終わっているようなものです!(^^)!
まずは力学的エネルギー保存則とは
《力学的エネルギー保存則》
(後の力学的エネルギー)=(前の力学的エネルギー)
です!
この式と『仕事と力学的エネルギーの関係式』を見比べてみればわかりますが、(非保存力がした仕事の和)がないだけです。
つまり、非保存力が仕事をしなければ力学的エネルギーは保存するということです。
もっというと、保存力のみが仕事をしていれば力学的エネルギーは保存するということです!
《力学的エネルギーが保存する条件》
保存力のみが仕事をするとき、力学的エネルギーは保存する。つまり
(後の力学的エネルギー)=(前の力学的エネルギー)
が成り立つ。
この条件を意識してみるといつ力学的エネルギー保存則が使えるかわかるね!
後は、使う練習をするだけだ!
力学的エネルギー保存則の使い方を具体例で解説!

以上で
- 仕事と運動エネルギーの関係式
- 仕事と力学的エネルギーの関係式
- 力学的エネルギー保存則
の説明を全てしたことになりますね!
- 仕事と運動エネルギーの関係式
- 仕事と力学的エネルギーの関係式
の2つは具体例を用いて説明したときに立式していますので、ここではそのうちの力学的エネルギー保存則の使い方を具体例を用いてみていきたいと思います!
具体例
(問題)
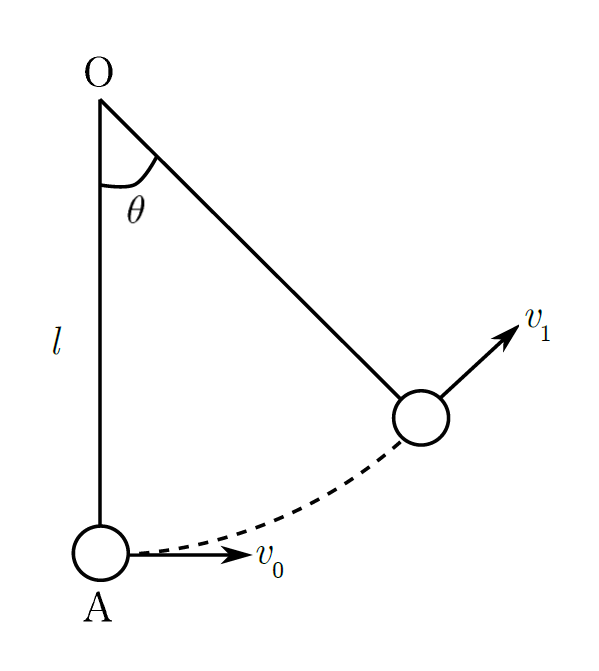
上図のように、点Oに長さが$l$で軽くて伸びない糸の一端を固定し、他端に質量$m$の小球を吊るす。点Oの鉛直下方の点Aで初速$v_{0}$を与え、鉛直方向となす角が$\theta$になったときの速さ$v_{1}$を$v_{0}$、$g$、$l$、$\theta$を用いて求めよ。ただし、重力加速度の大きさを$g$とする。
(解答)
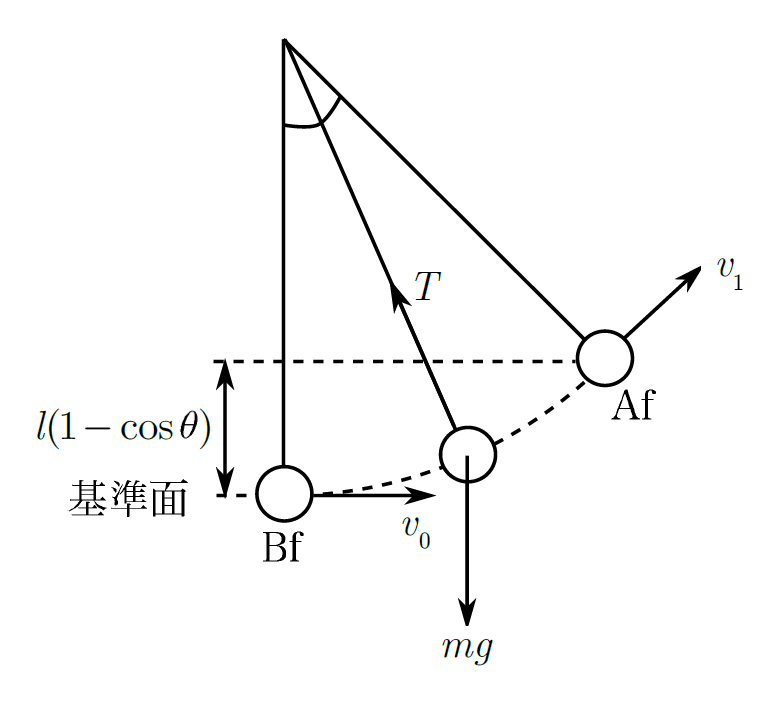
上図のように、点Aの位置を前(Bf)の位置で速さが$v_{1}$になった(角度が$\theta$)の位置を後(Af)とすると、BfからAfまでにはたらく力は重力$mg$と張力$T$の2つです。
- 張力$T$は小球の運動方向に対し常に垂直なので、張力の仕事は0。
- 重力$mg$は$-mgl(1-\cos\theta)$の仕事をしますが、重力$mg$は保存力なので、重力が仕事をしても力学的エネルギーは変化せず、保存される。
この2点から力学的エネルギー保存則が使える!
ではまずBfの力学的エネルギー$E_{\mathrm{Bf}}$についてみていきましょう
- 運動エネルギーは$\Large{\frac{1}{2}}$$mv_{0}^{2}$のみ。
- Bfの力学的エネルギー$E_{\mathrm{Bf}}$はBfの高さを基準面とすると、重力による位置エネルギーは0。
よって、Bfの力学的エネルギー$E_{\mathrm{Bf}}$は
$E_{\mathrm{Bf}}=\Large{\frac{1}{2}}$$mv_{0}^{2}$
次にAfの力学的エネルギー$E_{\mathrm{Af}}$についてみてきます。
- 運動エネルギーが$\Large{\frac{1}{2}}$$mv_{1}^{2}$。
- 基準面よりも$l(1-\cos\theta)$だけ高い位置に小球はいるので、重力による位置エネルギーは$mgl(1-\cos\theta)$。
よって、Afの力学的エネルギー$E_{\mathrm{Af}}$は
$E_{\mathrm{Af}}=\Large{\frac{1}{2}}$$mv_{1}^{2}+mgl(1-\cos\theta)$
以上から、力学的エネルギー保存則を立てると
$E_{\mathrm{Af}}=E_{\mathrm{Bf}}$
となるので、以上から
$\Large{\frac{1}{2}}$$mv_{1}^{2}+mgl(1-\cos\theta)=\Large{\frac{1}{2}}$$mv_{0}^{2}$
となるので、この式を変形すると、速さ$v_{1}$は
$v_{1}=\sqrt{v_{0}^{2}-2gl(1-\cos\theta)}$
となり、求められました。
必ず力学的エネルギー保存則が使えることを確認してみましょう!
そして、問題を見た瞬間に力学的エネルギー保存則が使えることがわかるようになればOKです!(^^)!
まとめ

以上で『【高校物理】力学的エネルギー保存則をわかりやすく解説!』を終わりにします!
この分野は【物理基礎】だけでなく、むしろ【物理】の分野でガンガン使うので、絶対にできるようにしておきましょう!
物理をできるようにするための方法を最後に確認しておきますが、
- 物理現象をしっかりと理解する。
- 問題演習を繰り返し行う。
この2点を行うことが必須です。
物理は最初ハードルが高いですが、この2点をしっかりやることでそのハードルを越えられて誰でも得意になれる科目なので根気強く勉強していきましょう!
また、このサイトでは物理の内容や、勉強法、おすすめの参考書や問題集も紹介していますので、是非読んでみてくださいね!










